9 Análisis Factorial Confirmatorio

El análisis factorial confirmatorio (AFC) es una técnica estadística que permite verificar si una estructura factorial teórica se configura en los datos observados. Una diferencia sustantiva con el AFE es que en el proceso de estimación del AFC se debe definir cómo se agrupan los ítems, mientras que en el AFE los resultados sugerían la estructura factorial de los datos.

El AFC permite obtener evidencias de validez de las interpretaciones de las puntuaciones basadas en la estructura interna, lo cual indica que los ítems se agrupan en la forma esperada según la teoría y por tanto, es razonable estimar puntuaciones de un factor subyacente a dichos ítems.

Ahora bien, el AFE y el AFC parecen tener las mismas implicaciones, no obstante, en el AFC se analiza la presencia de la estructura teórica en los datos, de forma fiel al modelo teórico; mientras que en el AFE se permite que los ítems aporten a otros factores que no son señalados en la teoría. En la práctica el AFE se utiliza para depurar un instrumento en sus versiones iniciales y el AFC se utiliza para mostrar que los ítems de un instrumento depurado presentan la estructura definida a nivel teórico.

9.1 Fórmula

En el AFC, las variables observadas se denominada indicadores y se representan como x_i, por su parte, los factores subyacentes a los conjuntos de ítems se denominan variables latentes exógenas y se representan como \xi_j. El AFC clásico plantea que cada ítem x_i es explicado por una variable latente y un error aleatorio asociado a la regresión del ítem sobre la variable latente (\varepsilon_i). Estas relaciones se plantean gráficamente con las siguientes condiciones:

Los ítems se representan con rectángulos.
Las variables latentes se representan con círculos grandes.
Los errores se representan con círculos pequeños.
Las regresiones se modelan con flechas de las variables latentes a los ítems correspondientes.
La presencia de errores de regresión se modelan con flechas de los errores a los ítems correspondientes.

En un grupo de 6 ítems, en el que se teoriza que hay un factor subyacente para los primeros tres ítems y otro para los segundos tres ítems , se tendría una estructura factorial de la siguiente forma:

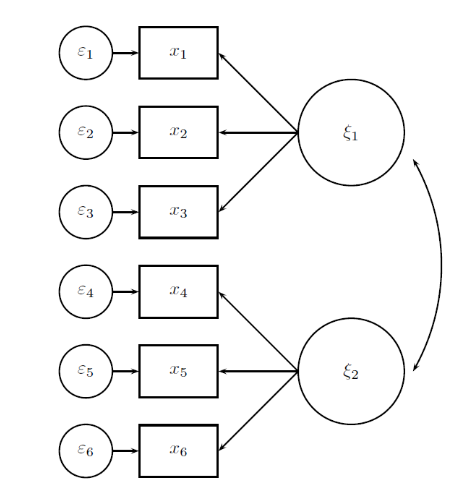
En esta estructura se puede observar que no hay flechas de \xi_1 a los ítems x_4, x_5 y x_6, esto se debe a que en la estructura teórica no se plantean esas relaciones; en cambio en el AFE sí se estiman dichas asociaciones.

Ahora bien, la fórmula matemática para un AFC con n items y m factores es la siguiente:

\begin{array}{ccc} x_1&=&\lambda_{11}^{x}\xi_1+\lambda_{12}^{x}\xi_2+...+\lambda_{1m}^{x}\xi_m+\varepsilon_1\\ x_2&=&\lambda_{21}^{x}\xi_1+\lambda_{22}^{x}\xi_2+...+\lambda_{2m}^{x}\xi_m+\varepsilon_2\\ x_3&=&\lambda_{31}^{x}\xi_1+\lambda_{32}^{x}\xi_2+...+\lambda_{3m}^{x}\xi_m+\varepsilon_3\\ x_4&=&\lambda_{41}^{x}\xi_1+\lambda_{42}^{x}\xi_2+...+\lambda_{4m}^{x}\xi_m+\varepsilon_4\\ &\vdots& \\ x_n&=&\lambda_{nm}^{x}\xi_1+\lambda_{n2}^{x}\xi_2+...+\lambda_{nm}^{x}\xi_m+\varepsilon_n\\ \end{array}

donde \lambda_{ij}^{x} representa el coeficiente de regresión de la variable x_i sobre la variable latente \xi_j y, \varepsilon_{i} representa el error asociado a la regresión de x_i (Rojas, 2020). Acá es importante mencionar que en las regresiones que no se plantean en la teoría, el coeficiente de regresión se fija en 0.

Por otro lado, el grupo de regresiones anteriores se puede simplificar a la siguiente forma matricial

\mathbf{x}=\bm\Lambda_x\bm\xi+\bm\varepsilon

Los coeficientes de regresión en el AFC se comportan de forma similar a las cargas factoriales del AFE, los valores cercanos a 1 indican que los ítems cargan en el factor teorizado y los cercanos a 0 indican que el ítem no carga en el factor.

9.2 Ejemplo de implementación del AFC

En el siguiente ejemplo se va a estimar un AFC en los datos de la escala GTAI. En esta escala se plantea que hay 4 dimensiones: preocupación, emocionalidad, interferencia y falta de confianza. En este ejemplo, vamos a suponer que la base de datos del repositorio es el resultado de una segunda aplicación de la GTAI depurada (sin los ítems EM7 y EM8) y reducida a las dimensiones de preocupación y emocionalidad. De esta manera, el AFC que se estudiará tendrá la siguiente estructura:

Los ítems PR1-PR9 cargan en el factor Preocupación.
Los ítems EM1-EM6 cargan en el factor Emocionalidad.

Las cargas factoriales de este AFC, se presentan en la última columna del siguiente cuadro:

   lhs op rhs   est    se      z pvalue std.all
1   PR =~ PR1 0.741 0.056 13.305      0   0.741
2   PR =~ PR2 0.797 0.043 18.625      0   0.797
3   PR =~ PR3 0.906 0.031 29.604      0   0.906
4   PR =~ PR4 0.700 0.053 13.253      0   0.700
5   PR =~ PR5 0.768 0.054 14.230      0   0.768
6   PR =~ PR6 0.873 0.033 26.805      0   0.873
7   PR =~ PR7 0.875 0.032 27.223      0   0.875
8   PR =~ PR8 0.867 0.032 27.303      0   0.867
9   PR =~ PR9 0.888 0.028 31.459      0   0.888
10  EM =~ EM1 0.776 0.044 17.464      0   0.776
11  EM =~ EM2 0.656 0.063 10.425      0   0.656
12  EM =~ EM3 0.425 0.086  4.925      0   0.425
13  EM =~ EM4 0.725 0.056 12.911      0   0.725
14  EM =~ EM5 0.861 0.048 18.110      0   0.861
15  EM =~ EM6 0.908 0.043 21.243      0   0.908

Nótese que las primeras 9 filas corresponden a los ítems de preocupación y las últimas 6 a los ítems de Emocionalidad. En todos los reactivos se obtienen cargas factoriales superiores a .35, las cuales indican que los ítems tienen una carga factorial relevante en el factor teorizado. Por tanto, se tiene una primera evidencia de que la estructura factorial se configura en los datos.

Las primeras columnas del cuadro corresponden a las salidas de la regresión lineal sin considerar la estandarización de los ítems, lo cual permite estudiar la influencia de un factor en un ítem considerando las unidades originales del reactivo.

9.3 Estimación de los coeficientes

La estimación del modelo de AFC se basa en el estudio de la matriz de varianzas observadas de los ítems (\mathbf{S}) y la matriz de varianzas estimada a partir de la estructura teórica (\hat{\bm\Sigma}). La estructura teórica de la matriz de correlaciones en el AFC es \bm\Sigma=\bm\Lambda_x\bm\Phi\bm\Lambda_{x}^{'}+\bm\Theta_\varepsilon, con \bm\Phi la matriz m \times m de variancias y covariancias de las variables latentes y \bm\Theta_\varepsilon, la matriz diagonal n \times n de variancias de los errores de las regresiones. Entonces, con base en la matriz estimada, se concluye que en el AFC también se estiman las varianzas y covarianzas entre las variables latentes y las varianzas de los errores de regresión.

Para la estimación de los coeficientes se buscan los parámetros que permitan que la matriz \hat{\bm\Sigma} se parezca lo mejor posible a la matriz \mathbf{S}. En el caso de los ítems ordinales (como los de escalas), para la determinación de los parámetros se acostumbra a utilizar un método de estimación denominado DWLS.

Otro elemento que se debe considerar en la estimación de los parámetros es la determinación de la métrica de las variables latentes. Esta puede ser establecida de dos formas:

Adoptando la métrica de un ítem asociado al factor.
Fijando la métrica en unidades estandarizadas (esto provoca que las varianzas de las variables latentes sean iguales a 1 y sus covarianzas se conviertan en correlaciones).

En el caso del AFC estimado en la GTAI se utilizó la segunda opción. Además, la correlación entre los factores fue

[1] 0.74

9.4 Los índices de ajuste

Los índices de ajuste del AFC brindan criterios para determinar qué tan bien se configuró el modelo teórico en los datos. Existen tres tipos de índices de ajuste:

De ajuste absoluto: Indican el grado de similitud entre la matriz de correlaciones observada y las correlaciones obtenidas en los datos con base en los parámetos estimados, lo cual se hace por medio del estudio de los residuos obtenidos. En este grupo están el root mean square error of approximation (RMSEA) y el Standardized Root Mean Square Residual (SRMR).
De ajuste incremental: Indican cuánto mejora el modelo en comparación con el modelo nulo (en el que los ítems no son explicados por ningún factor, es decir, su variabilidad es igual a la del error respectivo). En este grupo destacan el Comparative fit index (CFI) y el Tucker-Lewis Index (TLI).
De ajuste comparativo: Estos índices permiten determinar cuál de los modelos estimados presenta un mejor ajuste a los datos. Acá destacan el Akaike information criterion (AIC) y el Bayesian information criterion (BIC).

Una recomendación para concluir que un modelo AFC presenta un buen ajuste a los datos es que el SRMR sea menor a .08 y que el RMSEA sea menor a .06 o que el CFI sea mayor a .95 (Hu y Bentler, 1999).

En el ejemplo de estudio de la escala GTAI, se obtuvieron los siguientes índices de ajuste:

  cfi.scaled rmsea.scaled         srmr 
       0.977        0.074        0.074

9.5 Sintaxis en R

Cargar la base

BASE<-read.csv("GTAI19.csv",sep=",")

Cargar el paquete para Análisis Factorial Confirmatorio

install.packages("lavaan")
library(lavaan)

Sintaxis de lavaan

#La estructura del modelo de lavaan se digita en modo texto '' y
#se guarda en un objeto que va a ser llamada en la función de estimación

#El elemento básico del modelo de estructura del AFC corresponde a
#las regresiones de varios ítems (I1, I2) sobre una variable latente (VL)
VL=~I1+I2
#Los nombres de las variables latentes se definen en el modelo
#Los nombres de los ítems son iguales a los de la base

#Elementos adicionales que se pueden agregar al modelo, para fijar valores

#varianza de los errores de regresión
#Nota: Por defecto lavaan estima estas varianzas
I1~~I1
#Si se desea fijar esta varianza en 1 solo se multipla por la
#izquierda al último elemento por 1
I1~~1*I1

#Varianzas de las variables latentes
#Nota: Por defecto lavaan estima estas varianzas
VL~~VL

#Covarianzas de las variables latentes (VL, VL2)
#Nota: Por defecto lavaan estima estas varianzas
VL~~VL2

#Covarianzas de los errores de regresión
#Nota: Por defecto lavaan las fija en 0
#Si se agrega esta línea de código el software las estima
I1~~I2

#Umbral 1 de un ítem ordinal
#Nota: Por defecto lavaan estima estos umbrales
I1 | t1

#Umbral 2 de un ítem ordinal
#Nota: Por defecto lavaan estima estos umbrales
I1 | t2

#Media de una variable latente
#Nota: Por defecto lavaan estima estas medias
VL ~ 1
"

Estimación del modelo de AFC: Definición de la estructura

mod<-'
  PR=~PR1+PR2+PR3+PR4+PR5+PR6+PR7+PR8+PR9
  EM=~EM1+EM2+EM3+EM4+EM5+EM6'

#Los factores pueden llevar el nombre que se desee
#La sintaxis de lavaan es:
#Factor =~ Ind_1+Ind_2+...+Ind_n

Estimación del modelo

fit<-sem(mod, data=BASE, std.lv=T,ordered = TRUE)
#std.lv indica que la métrica de las variables latentes será la estandarizada
#ordered indica que los indicadores son politómicos

Coeficientes de los ítems e índices de ajuste

summary(fit, standardized=TRUE,fit.measures=T)
#standardized indica que se requieren los coeficientes estandarizados
#los coeficientes de regresión representan las cargas factoriales

9.6 Guía de trabajo 1

Para esta guía vamos a suponer que la base de datos del repositorio de la GTAI es el resultado de una segunda aplicación de la GTAI depurada (sin los ítems EM7 y EM8) y reducida a las dimensiones de falta de confianza e interferencia. De esta manera, el AFC que se estudiará tendrá la siguiente estructura:

Los ítems FC1-FC6 cargan en el factor Falta de Confianza.
Los ítems IN1-IN6 cargan en el factor Interferencia.

Con base en lo anterior, conteste lo siguiente:

¿Cuáles ítems presentaron cargas factoriales aceptables en los factores correspondientes? (2 pts)
Determine si hubo una correlación relevante entre las variables latentes consideradas (1 pto).
Use el SRMR para determinar si el modelo presentó un ajuste absoluto aceptable e interprete el valor de este coeficiente (2 pts).
Use el TLI para determinar si el modelo presentó un ajuste incremental aceptable e interprete el valor de este coeficiente (2 pts).
Determine si el modelo teórico se ajustó a los datos (1 pto)
Enuncie una conclusión asociada a la validez de las interpretaciones de las puntuaciones que se puede hacer a partir de los resultados obtenidos (cuidado con el lenguaje utilizado) (1 pto).

9.7 Índices de confiabilidad de los factores

El coeficiente omega indica el porcentaje de variabilidad de los ítems debida a la variabilidad del factor y es un índice de confiabilidad más apropiado para los ítems ordinales que el alfa de Cronbach. Este coeficiente indica qué tan confiable es la suposición de que las puntuaciones de estos ítems son generadas por un factor subyacente.

La fórmula se basa en calcular el porcentaje de variabilidad de los ítems debido a la variabilidad del factor y su representación es:

\omega=\frac{\left(\sum \lambda_i\right)^2}{\left(\sum \lambda_i\right)^2+\sum \theta_i} donde \lambda_i son las cargas factoriales de los ítems en el factor y \theta_i la varianza de los errores de regresión de los ítems sobre el factor de interés. Se considera que un índice omega es aceptable si su valor es mayor que .70 (Flora, 2020).

El average variance extracted (AVE) indica el porcentaje de varianza de la matriz estimada de varianza y covarianzas que es explicado por la variabilidad del factor. Este índice es relevante porque indica si las correlaciones estimadas dependen más de la variabilidad del factor, que de la variabilidad del error.

En el caso de los constructos estudiados en el ejemplo de este capítulo, se tienen los siguientes índices de confiabilidad:

          PR    EM
omega  0.920 0.814
avevar 0.684 0.551

Note que ambos constructos tienen evidencias de confiabilidad debido a que el coeficiente \omega indicó que el 92.0% y el 81.4% de la varianza de los ítems de Preocupación y Emocionalidad es explicada por la variabilidad del factor correspondiente. Por su parte, el AVE señaló que el 68.4% y el 55.1% de la variabilidad total de los ítems de Preocupación y Emocionalidad es explicada por la variabilidad del factor correspondiente.En ambos casos se observa que la variabilidad total de los ítems depende más del factor en estudio, que de los errores.

Ambos coeficientes indicaron evidencias de confiabilidad, debido a que se concluyó que la variabilidad de los reactivos está más asociada a la variabilidad del constructo subyacente, que a la variabilidad de los errores. Nota: No proporciona evidencias de validez debido a que estas propiedades no indican que se está midiendo el constructo de interés, si no que se está midiendo con una precisión apropiada el un constructo subyacente.

9.8 Invarianza factorial

La invarianza factorial es una propiedad de las variables latentes que indica que varios de sus coeficientes se definen de forma similar en grupos de población establecidos. La relevancia de esta propiedad es que permite determinar a) si el constructo de interés tiene el mismo significado en dos grupos de interés y b) si tiene sentido comparar las puntuaciones estimadas por individuos en dos grupos de población.

Los tipos de coeficientes con valores similares entre grupos determinan los niveles de invarianza, los cuales son:

Invarianza configural: El modelo en el que se propone que un grupo de ítems carga en un factor presenta un ajuste aceptable en los grupos de interés.
Invarianza débil o métrica: Las cargas factoriales son iguales en los grupos de interés.
Invarianza fuerte o escalar: Las cargas factoriales y los umbrales son iguales en los grupos de interés.
Invarianza estricta: Las cargas factoriales, los umbrales y la varianza de los errores de regresión son iguales en los grupos de interés.

Ahora bien, las implicaciones prácticas en la estructura y medición de los constructo debidas a estos niveles de invarianza son las siguientes:

Invarianza configural: Se puede concluir que en los grupos de interés, se configuran las variables latentes esperadas.
Invarianza débil o métrica: Se puede concluir que en los grupos de interés, el constructo estudiado presenta la misma estructura de coeficientes de regresión. En consecuencia, los reactivos que tengan más peso en la definición de las puntuaciones del constructo serán los mismos en todos los grupos de interés.
Invarianza fuerte o escalar: Se puede concluir que en los grupos de interés, los ítems y el constructo estudiado presentan la misma métrica. Por tanto, tiene sentido comparar las puntuaciones obtenidas en el constructo por individuos de distintos grupos.
Invarianza estricta: Se puede concluir que el constructo presenta la misma precisión en los grupos de interés.

Nota: Las consecuencias inmediatas de la invarianza se observan en las medidas de los ítems; no obstante, para propósitos de medición devariables latentes importa ver las consecuencias secundarias en las medidas de las variables latentes.

9.9 Estimación de la invarianza

En la construcción de la estructura de los modelos de invarianza se debe definir una estructura base que se estimará en dos o más grupos simultáneamente, la cual representa la estructura de interés que se analiza en los modelos con toda la población. Este análisis se denomina modelo multigrupo.

Luego de crear la estructria base, se suele fijar la métrica de las variables latentes usando un ítem guía en cada factor, en lugar de fijar la varianza de estos. En el modelo de invarianza débil se establece que las cargas factoriales son iguales entre grupos y en el modelo de invarianza fuerte se fijan las cargas factoriales y los umbrales (en cada ítem ordinal se supone que existe una variable normal subyacente a este, los umbrales indican los valores de la variable subyacente que determinan la asignación de valores ordinales).

Millsap and Yun-Tein (2004) y Pornprasertmanit (2022) señalan que para estimar la invarianza en ítems politómicos, además de los elementos indicados se deben considerar los siguientos aspectos:

Un umbral de cada variable es fijado entre grupos ( x1|c(u1,u1)*t1 ). Note que esta condición impide el cálculo de invarianza fuerte en los ítems dicotómicos.
En los ítems guía se debe fijar un umbral adicional ( x1|c(u2,u2)*t2 ).
Las varianzas del error de los ítems del grupo 1 se fijan en 1 (parameterization = “theta”).
Las medias de los factores en el primer grupo son fijadas a 1 ( f1 ~ c(0, NA)*1 ).

En el caso de ítems dicotómicos también se fijan las varianzas del error de los ítems guía del segundo grupo ( x1 ~~ c(1, 1)*x1 ), ya que acá no se puede fijar un umbral adicional en los ítems guía (Rojas-Torres et al., 2018). Además, las condiciones anteriores implicar que en estos ítems no se pueda calcular invarianza fuerte.

Una vez definida la estructura de los modelos de invarianza, se estima el ajuste de estos modelos a los datos. Se considera que el modelo de invarianza configural se ajusta a los datos si presenta los valores de los índices de ajuste mencionados en los modelos con un solo grupo. Se acepta un modelo de invarianza superior, si su CFI menos el CFI previo (\Delta\text{CFI}) es mayor que -.01 unidades. Otro criterio para aceptar un nivel de invarainza superior es que el el \Delta\text{RMSEA}<.015 (Chen, 2007; Férnandez et al, 2023).

9.10 Ejemplo de la implementación de un análisis de invarianza

En el siguiente ejemplo se estudiará el modelo de AFC con las variables latentes Preocupación y Emocionalidad. Antes de empezar el análisis de invarianza se recomienda análizar el ajsute del modelo en cada grupo por separado. En este caso se obtuvieron los siguientes índices de ajuste:

     cfi.scaled rmsea.scaled  srmr
Masc      0.991        0.045 0.093
Fem       0.954        0.101 0.113

Se puede observar que el ajuste en los hombres fue aceptable, mientras que en las mujeres estuvo un poco distante a lo esperado. No obstante, se va a considerar aceptable para estudiar los niveles siguientes. Ahora bien, los índices de ajuste en cada uno de los modelos de invarianza fueron los siguientes:

    CFI   DCFI RMSEA DRMSEA  SRMR
1 0.970     NA 0.078     NA 0.106
2 0.964 -0.006 0.083  0.005 0.130
3 0.966  0.002 0.081 -0.002 0.107
4 0.963 -0.003 0.081  0.000 0.130

Nótese que el modelo inicial presentó un ajuste aceptable, considerando el RMSEA y el CFI (aunque no se cumplió el criterio clásico del SRMR). Luego, todos los \Delta\text{CFI} fueron mayores que -.01 y que todos los \Delta\text{RMSEA} fueron menores que .015, por tanto, se puede llegar hasta el último nivel de invarianza.

Entonces se puede concluir que: a) los ítems tienen los mismos aportes en las mediciones de los constructos, tanto en hombres como en mujeres (invarianza débil), b) los constructos poseen las mismas métricas entre hombres y mujeres (invarianza fuerte) y c) los constructos poseen la misma precisión en los grupos de interés (invarianza estricta).

Por último, dado que se alcanzó la invarianza fuerte se puede estudiar la diferencia de promedios entre hombres y mujeres en las variables latentes de interés. En el caso de interés se obtuvo que las d de Cohen fueron de -.57 y -.75 en Preocupación y Emocionalidad, en contra de las mujeres.

9.11 Sintaxis en R

Cargar la base

BASE<-read.csv("GTAI19.csv",sep=",")

Cargar el paquete para análisis factorial confirmatorio y un paquete para análisis complementarios al AFC

library(lavaan)
install.packages("semTools")
library(semTools)

Definición de la estructura del modelo de AFC

mod<-'
  PR=~PR1+PR2+PR3+PR4+PR5+PR6+PR7+PR8+PR9
  EM=~EM1+EM2+EM3+EM4+EM5+EM6'

Estimación del modelo

fit<-sem(mod, data=BASE, std.lv=T,ordered = TRUE)

Estimar coeficientes de confiabilidad

reliability(fit)

Estimación del modelo en cada grupo de interés

#Definición de subconjuntos por grupos de interés
BASEM<-subset(BASE,sex=='M')
BASEF<-subset(BASE,sex=='F')

#Estimación del modelo
fitM <- cfa(mod, data = BASEM,ordered=T)
fitF <- cfa(mod, data = BASEF,ordered=T)

#Índices de ajuste
Masc<-round(fitMeasures(fitM)[c("cfi.scaled","rmsea.scaled","srmr")],3)
Fem<-round(fitMeasures(fitF)[c("cfi.scaled","rmsea.scaled","srmr")],3)

rbind(Masc, Fem)

Sintaxis de modelos multigrupo de lavaan

#En los modelos multigrupos los nombres de los coeficientes se definen con
#el formato de vector numérico  [ c(a1,a2,a3) ] y se unen con una multiplicación por
#la izquierda al elemento del modelo en el que se desea especificar los nombres de los coeficientes

#En un modelo con dos grupos en el que el coeficiente de regresión de I2 entre
#dos grupos se desea igual se puede poner la siguiente sintaxis
VL=~I1+c(a3,a3)*I2
#usar el mismo nombre de coeficiente le indica a lavaan que son iguales

#Ejemplo: umbral 1 igual entre grupos
I1 | c(u1, u1)*t1

#Ejemplo: umbral 3 igual entre grupos
I1 | c(u2, u2)*t2

#Ejemplo: medias iguales entre grupos
VL ~ c(m1, m2)*1

Definición de la estructura del modelo base de AFC para invarianza en ítems politómicos. Acá no hace falta fijar las cargas factoriales, umbrales o varianzas del error, pero si se deben agregar las condiciones para la definición del modelo en ítems dicotómicos.

mod <- "
#modelo base
PR=~PR1+PR2+PR3+PR4+PR5+PR6+PR7+PR8+PR9
EM=~EM1+EM2+EM3+EM4+EM5+EM6

#aspecto 1: umbrales de todos los ítems fijo entre grupos: 
PR1 | c(u1, u1)*t1 
PR2 | c(u2, u2)*t1 
PR3 | c(u3, u3)*t1 
PR4 | c(u4, u4)*t1 
PR5 | c(u5, u5)*t1 
PR6 | c(u6, u6)*t1 
PR7 | c(u7, u7)*t1 
PR8 | c(u8, u8)*t1 
PR9 | c(u9, u9)*t1 
EM1 | c(u10, u10)*t1 
EM2 | c(u11, u11)*t1 
EM3 | c(u12, u12)*t1 
EM4 | c(u13, u13)*t1 
EM5 | c(u14, u14)*t1 
EM6 | c(u15, u15)*t1 

#aspecto 2: umbral adicional en los ítems guía fijo entre grupos: 
PR1 | c(u16, u16)*t2
EM1 | c(u17, u17)*t2

#aspecto 3: varianzas del error del primer grupo fijas en 1. No hace falta agregar sintaxis,
#ya que la opción parameterization="theta" agrega esta condición

#aspecto 4: medias fijas en el primer grupo de las variables latentes
PR ~ c(0, NA)*1
EM ~ c(0, NA)*1
"

Modelos multigrupo para el análisis de invarianza

#Base con solo los grupos de interés
BASE0<-rbind(BASEM,BASEF)

#Estimación de los modelos
fit0 <- cfa(mod, data = BASE0, group = "sex", parameterization="theta", estimator="wlsmv")
fit1 <- cfa(mod, data = BASE0, group = "sex", parameterization="theta", estimator="wlsmv", group.equal = c("loadings"))
fit2 <- cfa(mod, data = BASE0, group = "sex", parameterization="theta", estimator="wlsmv",group.equal = c("loadings","thresholds"))
fit3 <- cfa(mod, data = BASE0, group = "sex", parameterization="theta", estimator="wlsmv",group.equal = c("loadings","thresholds","residuals"))

Índices de ajuste de los modelos de invarianza

x1<-fitMeasures(fit0)[c("cfi.scaled","rmsea.scaled","srmr")]
x2<-fitMeasures(fit1)[c("cfi.scaled","rmsea.scaled","srmr")]
x3<-fitMeasures(fit2)[c("cfi.scaled","rmsea.scaled","srmr")]
x4<-fitMeasures(fit3)[c("cfi.scaled","rmsea.scaled","srmr")]

CFI<-c(x1[1],x2[1],x3[1],x4[1])
DCFI<-c(NA, x2[1]-x1[1],x3[1]-x2[1],x4[1]-x3[1])
RMSEA<-c(x1[2],x2[2],x3[2],x4[2])
DRMSEA<-c(NA, x2[2]-x1[2],x3[2]-x2[2],x4[2]-x3[2])
SRMR<-c(x1[3],x2[3],x3[3],x4[3])

data.frame(CFI,DCFI,RMSEA,DRMSEA,SRMR)

Estudio de los resultados del modelo de invarianza fuerte

summary(fit2,standardized=T)

9.12 Guía de trabajo 2

Los ítems FC1-FC6 cargan en el factor Falta de Confianza.
Los ítems IN1-IN6 cargan en el factor Interferencia.

Con base en lo anterior, conteste lo siguiente:

¿Cuáles son los valores de los índices de confiabilidad de los factores correspondientes? (2 pts)
Concluya si hay o no evidencias de confiabilidad de los constructos estudiados (2 pts).
Determine si el modelo base presenta un ajuste apropiado en cada uno de los grupos estudiados (2 pts)
Presente los índices de ajuste de los modelos de invarianza (2 pts).
Concluya el nivel de invarianza alcanzado con el criterio del CFI (1 pto).
Determine cuáles conclusiones se pueden hacer sobre el comportamientos de los constructos entre grupos (1 pto)
Determine si hay diferencias entre género de las variables latentes involucradas (1 pto).

9.13 Referencias

Flora DB. Your Coefficient Alpha Is Probably Wrong, but Which Coefficient Omega Is Right? A Tutorial on Using R to Obtain Better Reliability Estimates. Advances in Methods and Practices in Psychological Science. 2020;3(4):484-501. doi:10.1177/2515245920951747

https://sunthud.com/media/Teaching/SEM/catInvariance/catInvariance2.R