3  Teoría Clásica de los Test

3.1 El modelo

El modelo de la Teoría Clásica de los Test, está dado por la ecuación

\[X= V+\varepsilon\]

donde \(X\) representa la puntuación observada el test, mientras que \(V\) y \(\varepsilon\) representan dos variables no observadas denominadas la puntuación verdadera y el error de medida (Spearman).

La puntuación verdadera \(V\) es un constructo que representa el nivel del individuo en en el test.

El error de medida representa la desviación aleatoria de la puntuación verdadera respecto a la observada. Como consecuencia de la definición de \(V\), se tiene que \(E(\varepsilon)=0\).

Discusión

• ¿Por qué la puntuación verdadera generalmente no coincide con la puntuación observada?

• ¿Cuáles son las fuentes de error que pueden afectar la medición?

3.1.1 Supuestos teóricos

• La esperanza de la puntuación observada es la puntuación verdadera (\(E(X)=V\)).

• La correlación entre las puntuaciones verdaderas y los errores es 0 (\(\rho_{V\varepsilon}=0\)).

• La correlación entre los errores obtenidos en dos mediciones del constructo es 0 (\(\rho_{\varepsilon_1\varepsilon_2}=0\)).

• Los errores derivados de la puntuación observada \(X_i\) tienen una distribución Normal de media \(0\) y varianza \(\sigma^2\) (\(\varepsilon_{X_i}\sim N(0,\sigma^2)\)).

Discusión

• ¿Tienen sentido los primeros dos supuestos?

• ¿Tienen la misma variabilidad los errores derivados de 10 puntos y 19 puntos en un examen de 20 puntos?

3.1.2 Test paralelos

Dadas dos formas de un test, si en cada una de ellas los individuos tienen iguales puntuaciones verdaderas y varianzas de los errores, entonces estas se denominan formas paralelas. El concepto de los test paralelos permite obtener muchas de las propiedades de la TCT.\

En la práctica las fórmulas paralelas se basan en conjunto de ítems con estadísticas registradas, las cuales permiten diseñar ítems lo más semejantes posibles.

3.2 Coeficiente de fiabilidad

El coeficiente de fiabilidad (\(\rho_{XX'}\)) corresponde a la correlación entre las puntuaciones obtenidas en dos test paralelos \(X\) y \(X'\). También se interpreta como la proporción de la varianza de las puntuaciones observadas debida a la variación de las puntuaciones verdaderas.

Este coeficiente se utiliza en:

• El análisis de la fiabilidad del test.
• El cálculo de los intervalos de confianza de la puntuación verdadera de los individuos.

La raíz cuadrada de \(\rho_{XX'}\) se denomina índice de fiabilidad (\(\rho^2_{VX}\)) y representa la correlación entre las puntaciones verdaderas y las observadas:

\[\rho_{VX}=\sqrt{\rho_{XX'}}\]

3.2.1 Aproximaciones del coeficiente de fiabiliadad

Aproximación formas paralelas Es la correlación de las puntuaciones de dos formas paralelas.

Aproximación Test-Retest Es la correlación de las puntuaciones de dos formas idénticas aplicadas dos veces.

Aproximación dos mitades (half split) Se basa en dividir el test en dos mitades paralelas.

Su fórmula es:

\[\rho_{XX'}=\frac{2\rho_{H_1H_2}}{1+\rho_{H_1H_2}}\]

Aproximación alfa de Cronbach Se basa en las correlaciones de cada pareja de ítems. No demanda considerar fórmulas paralelas. Es una cota inferior del coeficiente de fiabilidad.

\[\alpha=\frac{n\frac{1}{K}\sum_{i<j}\rho_{x_ix_j}}{1+ (n-1)\frac{1}{K}\sum_{i<j}\rho_{x_ix_j}} = \frac{n}{n-1}\left(1- \frac{\sum \sigma^2_{x_i}}{\sigma^2_X}\right)\]

El \(\alpha\) también se suele interpretar como el grado de consistencia interna de los ítems, es decir, el grado de concordancia de las variaciones de las puntuaciones de los ítems.

Los rangos de interpretación del alfa son los siguientes:

• \(\alpha<.5\) inaceptable
• \(\alpha \geq.5\) pobre
• \(\alpha\geq.6\) cuestionable
• \(\alpha\geq.7\) aceptable
• \(\alpha\geq.8\) bueno
• \(\alpha\geq.9\) excelente (George y Mallery, 2003)

3.2.2 Ejemplo

En el caso de la dimensión Preocupación de la GTAI se tiene que el coeficiente de dos mitades fue:

[1] 0.911676

En el caso de la dimensión Preocupación de la GTAI se tiene que el alfa de Cronbach fue de:

[1] 0.9041099

Si se considera que el coeficiente de confiabilidad es .904, entonces, la proporción de la varianza de las puntuaciones observadas debido a las puntuaciones verdaderas sería 90.4%. Por otro lado, el índice de fiabilidad será:

round(sqrt(.904),2)

[1] 0.95

Por tanto, se concluye que la correlación entre la puntuación observada y la verdadera es de .951.

3.3 Análisis de los ítems

Los pasos iniciales para la estimación de las puntaciones verdaderas de los individuos son: 1) seleccionar los ítems que evalúan el constructo pretendido y 2) seleccionar los ítems que presentan las mejores propiedades para estimar las puntuaciones verdaderas.

3.3.1 Media de los ítems / Índice de dificultad (ID)

El promedio de los ítems brinda una aproximación a la respuesta representativa de la pregunta en la población. En el caso de los ítems dicotómicos se denomina índice de dificultad e indica la proporción de personas que acertaron el ítem:

\[ID=\frac{A}{N}\] Los valores altos del índice indican un alto acuerdo con la afirmación evaluada o que el ítem es muy fácil (en ítems dicotómicos). Los ítems con promedios o dificultades extremas generalmente son inapropiados para la estimación de las puntuaciones verdaderas, ya que no brindan margen para diferenciar a los individuos.

Entre las desventajas que presenta este índice están:

• Dependencia de la muestra utilizada.
• En pruebas de selección de respuesta, el valor puede aumentar debido al azar.

3.3.2 Índice de discriminación

El índice de discriminación es una medida de asociación entre las puntuaciones del ítem y la puntuación total. Entre más alto es el índice se puede concluir que el ítem separa mejor las personas con niveles altos de aquellas con niveles bajos en el constructo evaluado. El índice de correlación más utilizado es el denominado biserial-puntual (\(\rho_{pbis}\)), el cual es la adaptación de la correlación de Pearson con una variable ordinal. El límite inferior de la discriminación, por lo general, es 0.20.

3.3.3 Índice alfa de Cronbach reducido

El índice alfa de Cronbach reducido es el valor del alfa de Cronbach sin el ítem de interés. Si este índice es más bajo que el alfa de crobach original señala que el ítem tiene un aporte a la confiabilidad del test. Si es más alto quiere decir que el ítem perjudica la confiabilidad del test.

3.3.4 Ejemplo

En el caso de la dimensión Preocupación de la GTAI, se tiene que el análisis paralelo indicó la presenca de un único factor:

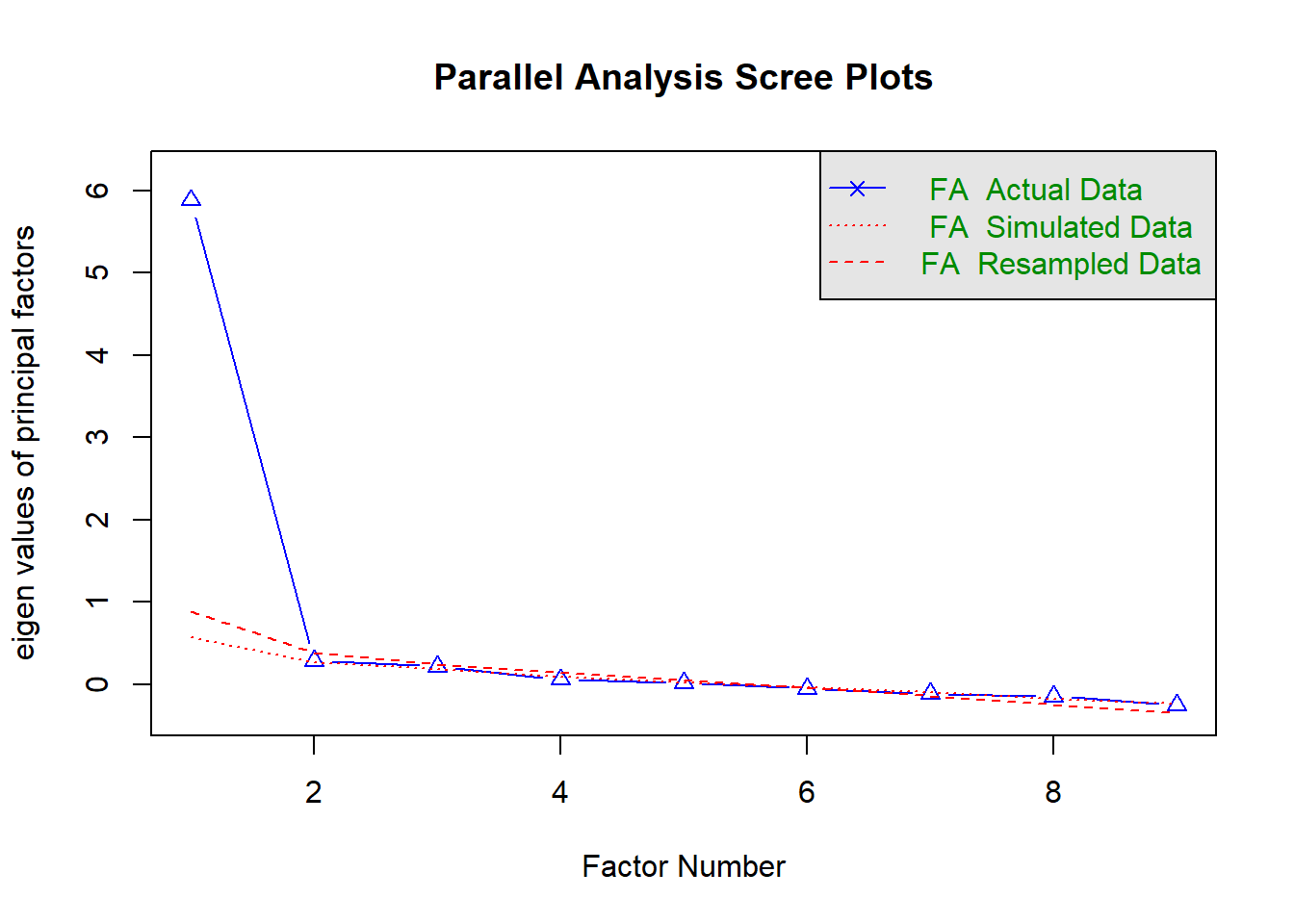
Parallel analysis suggests that the number of factors =  1  and the number of components =  NA 

Además, todos los ítems presentaron cargas relevantes en el factor

       lambda
PR1 0.7469009
PR2 0.7777563
PR3 0.8720138
PR4 0.6651126
PR5 0.7957180
PR6 0.8758110
PR7 0.8745819
PR8 0.8276347
PR9 0.8174857

En cuanto al análisis de ítems se obtuvieron los siguientes estadísticos

    Media Discrim Alfa red
PR1  1.72    0.64     0.90
PR2  1.07    0.75     0.89
PR3  1.34    0.83     0.88
PR4  1.26    0.67     0.90
PR5  1.67    0.69     0.90
PR6  1.53    0.81     0.89
PR7  1.39    0.81     0.89
PR8  1.18    0.78     0.89
PR9  1.23    0.79     0.89

En conclusión, todos los ítems pueden ser considerados para la estimación de las puntuaciones verdaderas. Por lo cual, la estimación del coeficiente de confiabilidad que se utilizará será el alfa de Cronbach calculado originalmente (\(.904\)). No se utilizará el coeficiente de dos mitades debido a que las mitades no fueron diseñadas con un modelo de paralelismo.

3.4 Intervalo de confianza de las puntuaciones verdaderas

El intervalo de confianza de una puntuación verdadera de un individuo viene dada por la fórmula: \[IC_{100(1-\alpha)\%}V=X\pm Z_{1-\alpha/2}\hat{\sigma}_\varepsilon\] con \(\hat{\sigma}_\varepsilon\), denominado error típico de medida, igual a:

\[\hat{\sigma}_\varepsilon=\hat{\sigma}_X\sqrt{1-\hat{\rho}_{XX'}}\] Note que entre más alto es el coeficiente de confiabilidad, menor es el error típico de medida; en cambio si el coeficiente es muy bajo, el error típico de medida crece hacia la desviación estándar de las puntuaciones observadas y por ende, a dar intervalos de confianza con longitudes casi iguales al rango total de variación del test.

3.4.1 Ejemplo

El individuo 2 de la base de datos de la GTAI obtuvo una puntuación de \(X=13\), en una escala de 0 a 18. Para calcular el intervalo de confianza del 95% de la puntuación verdadera de este individuo se requieren la desviación estándar de las puntuaciones observadas y la aproximación del coeficiente de confiabilidad (\(.904\), con base en el alfa de Cronbach). La desviación estándar de las puntuaciones observadas es

[1] 4.701821

Luego, ekl error típico de medición () esto esla desviación estándar del error de medición) equivale a

sigmaE<-sigmaX*sqrt(1-.904)
sigmaE

[1] 1.456806

Finalmente, los límites del intervalo de confianza serían:

\[IC_{100(1-.05)\%}V=13\pm 1.96 \cdot 1.47 = 13 \pm 2.88 \] Con lo cual el intervalo de confianza correspondería a: \[IC_{95\%}V = \left[10.12, 15.88\right]\]

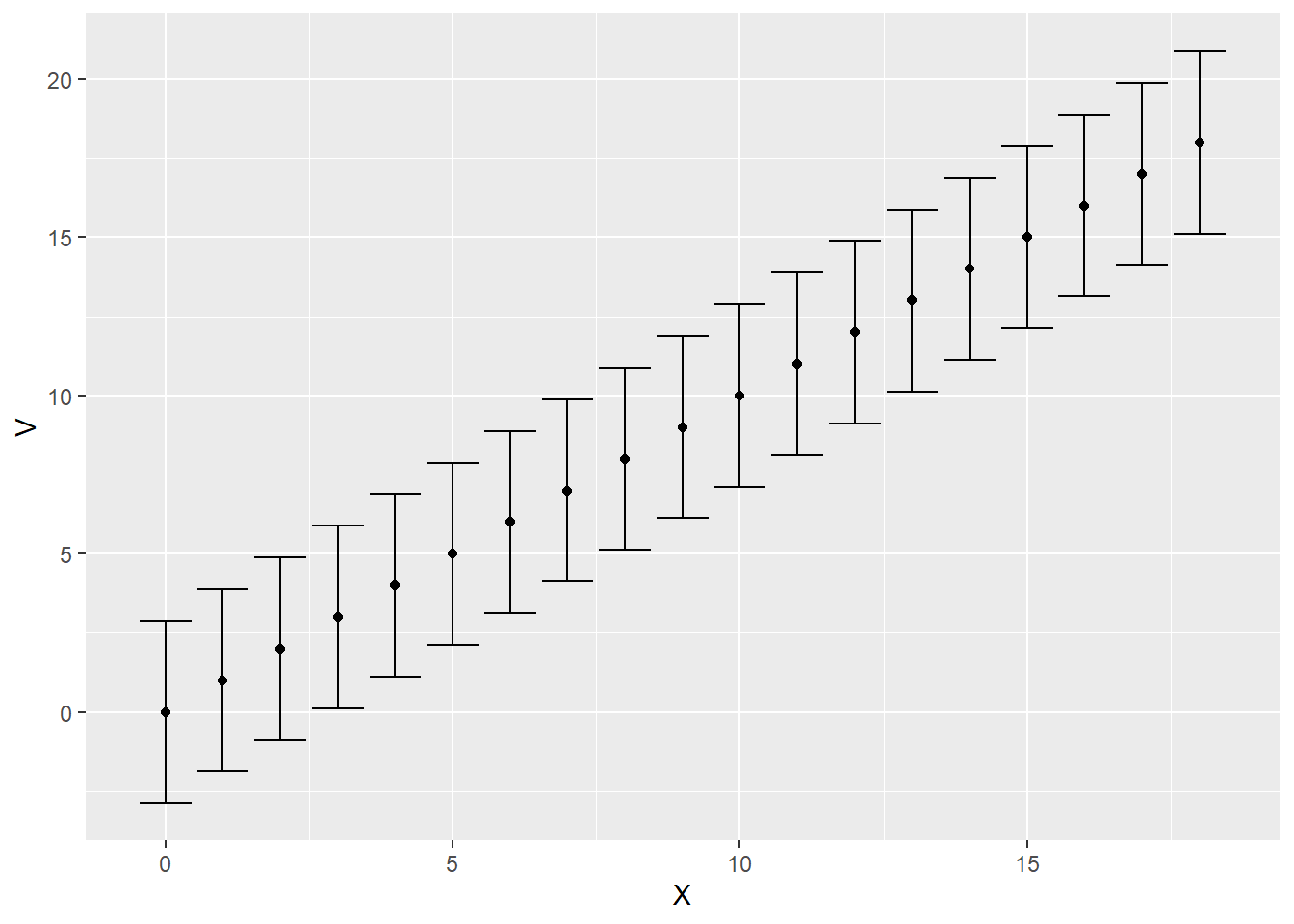
Finalmente, se puede concluir que todas los intervalos de confianza tendrían el mismo radio de 2.88 unidades, por lo cual los intervalos de confianza tendrían esta representación:

3.5 Análisis de datos con R

Importación de los datos

GTAI<-read.csv("GTAI19.csv",sep=",") ## ESCPECIFICAR DIRECCIÓN
PR<-GTAI[,c(2,5,8,9,13,16,20,22,26)] ## ESPECIFICAR ÍTEMS DE INTERÉS

Análisis de la unidimensionalidad y estructura factorial

library(psych)
fa.parallel(PR,fa="fa", cor="poly")

###
R<-polychoric(PR)
fit<- fa(R$rho, nfactors=1, fm="wls")
lambda<-fit$loadings[1:9,]            ### ESPECIFICAR NUM ÍTEMS
data.frame(lambda)

Análisis de los ítems

PR<- PR[ ,c(1:9)]       ## DEFINIR ÍTEMS ACEPTADOS EN EL AFE

library(psychometric)
stats<-item.exam(PR)
alfared<-psych:: alpha(PR)$alpha.drop[,1]
df<-data.frame(stats[,c(4,2)],alfared)
names(df)<- c("Media","Discrim","Alfa red")
round(df,2)

Coeficiente de confiabilidad con los ítems finales

PR<- PR[ ,c(1:9)]       ## DEFINIR ÍTEMS ACEPTADOS EN EL ANÁLISIS DE ÍTEMS

##Half-split
PRa<-PR[,c(1,3,5,7,9)]        ## DEFINIR ÍTEMS DE LAS MITADES
PRb<-PR[,c(2,4,6,8)]        ## DEFINIR ÍTEMS DE LAS MITADES
PRas<-rowSums(PRa)
PRbs<-rowSums(PRb)
r<-cor(PRas,PRbs,use="pairwise")
R<- 2*r/(1+r)
R

##Alfa
library(psychometric)
psychometric::alpha(PR)

Intervalo de confianza

conf<- .95        ##DEFINIR CONFIANZA
Z<- qnorm(conf)
X<-rowSums(PR, na.rm=T)
sigmaX<-sd(X,na.rm=T)
sigmaE<-sigmaX*sqrt(1-.904)
radio<-Z*sigmaE
radio

3.6 Guía de trabajo 2

Para la siguiente guia de trabajo considere los ítems 4, 8, 12, 17, 18 y 21 de la EAAE, asociados a la dimensión Puesta en Perspectiva del Afrontamiento.

1. Justifique por qué la subescala es unidimensional y determine cuáles ítems conforman el factor subyacente [2 puntos].

2. Presente la media, el índice de discriminación y el alfa reducido para los ítems seleccionados. [1 punto]

3. Indique si algún ítem debe ser eliminado o si todos deben mantenerse, con base en la media. Justifique su respuesta [1 punto].

4. Indique si algún ítem debe ser eliminado o si todos deben mantenerse, con base en la discriminación. Justifique su respuesta [1 punto].

5. Indique si algún ítem debe ser eliminado o si todos deben mantenerse, con base en el alfa reducido. Justifique su respuesta [1 punto].

6. Calcule el alfa de Cronbach para los ítems seleccionados finalmente y concluya el nivel de consistencia interna de la subescala [1 punto].

7. Considere el alfa de Cronbach como el estimador del coeficiente de confiabilidad. ¿Cuál es el porcentaje de varianza explicada de las puntuaciones observadas debido a las puntuaciones verdaderas? [1 punto]

8. Calcule el intervalo de confianza para una persona con una puntuación observada de \(6\) unidades [4 puntos].

3.7 Referencias

George, D., & Mallery, P. (2003). SPSS for Windows step by step: A simple guide and reference. 11.0 update (4th ed.). Allyn & Bacon.