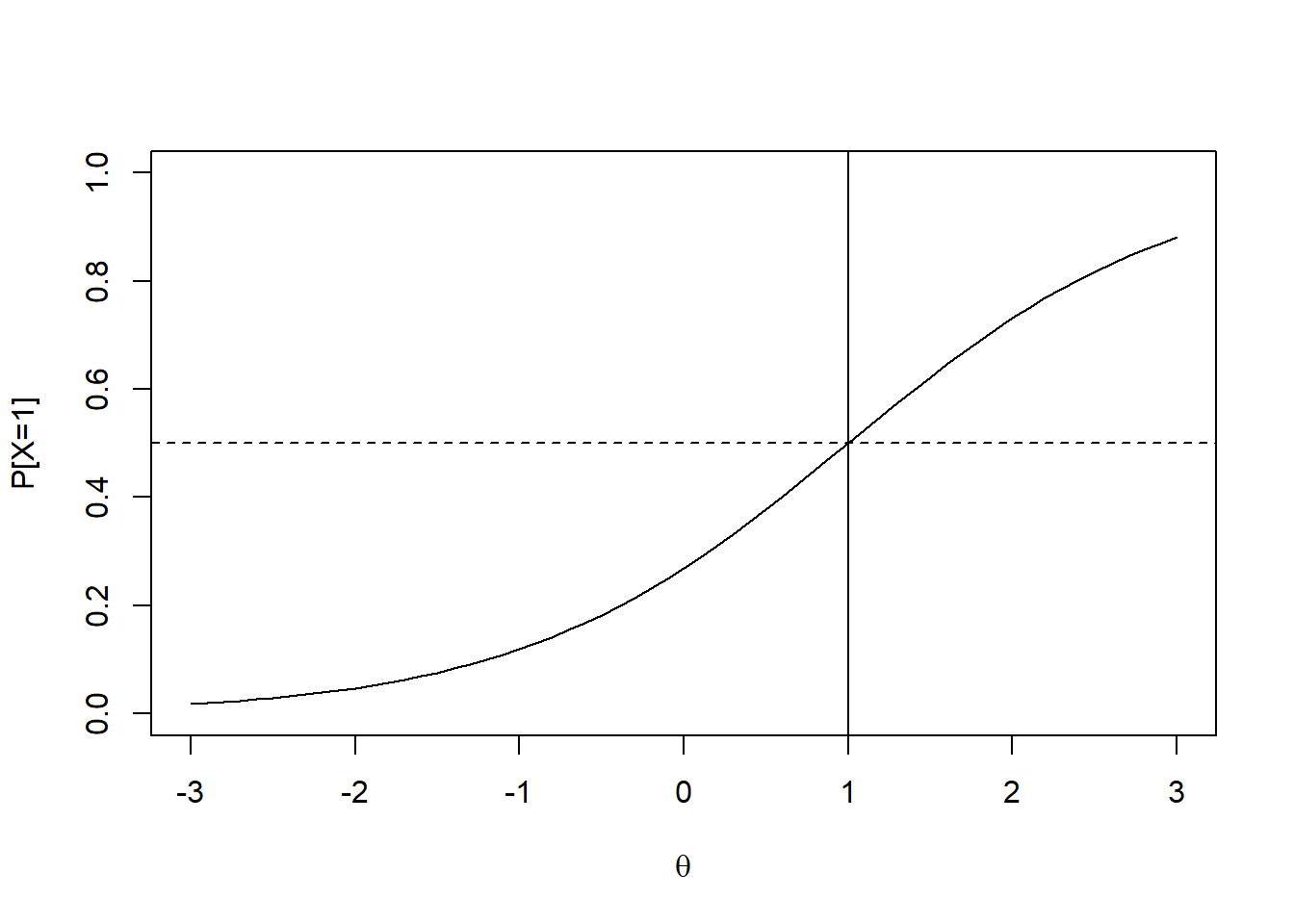
6 Modelo de Rasch
6.1 Descripción del modelo de Rasch
El modelo de Rasch es un modelo de medición de variables latentes que estima la habilidad de los individuos en función de la puntuación total observada. Para el estudio de las propiedades de los ítems y las personas utiliza una fórmula para cada ítem, en la que modela la probabilidad de respuesta del ítem en función de la habilidad de las personas y un parámetro de los ítems.
A diferencia de la TCT, este modelo a) usa una escala distinta (logits normalizados), b) brinda estimaciones de los parámetros de los ítems y las personas independientes de la población utilizada o los ítems utilizados, respectivamente y c) no asume que el test es igual de preciso para todo los niveles de habilidad.
Este modelo se caracteriza por el uso del ajuste de los datos al modelo, es decir, que analiza si los datos observados se ajustan a las propiedades esperadas por el modelo planteado.
6.1.1 Paso de puntuaciones totales a logits
Un problema que subyace al uso de las puntuaciones totales como mediciones de la habilidad es que no satisfacen el supuesto de la normalidad. Lo anterior se manifiesta al observar que dos puntuaciones consecutivas muy frecuentes tienen la misma separación que dos puntuaciones consecutivas poco frecuentes; en una escala normal, las primeras deberían estar más cerca que las segundas.
El modelo de Rasch busca obtener una mejor representación de las habilidades de los sujetos, por medio del uso de una escala con unidades logit. La transformación logit de una probabilidad es la siguiente
\[\theta= \ln\left(\frac{p}{1-p}\right)\]
En una estimación inicial de las habilidades de los sujetos, se realiza una transformación logit de las proporciones de respuestas observadas. Esto implica que:
- Las diferencias en las puntuaciones logit serán grandes para proporciones de respuestas observadas altas. Por ej. si \(p_1=.95\) y \(p_2=.90\), se tiene que \(\theta_1=2.95\) y \(\theta_2=2.18\), lo cual da una diferencia de .77 logits.
- Las diferencias en las puntuaciones logit serán pequeñas para proporciones de respuestas observadas medias. Por ej. si \(p_1=.50\) y \(p_2=.55\), se tiene que \(\theta_1=0\) y \(\theta_2=0.20\), lo cual da una diferencia de .20 logits.
Es importante mencionar que esta transformación no es la habilidad estimada por el modelo de Rasch. La habilidad final se obtiene luego de aplicar un método estadístico que permite obtener los parámetros de habilidad que mejor se ajustan a los datos observados, pero manteniendo la lógica de la medición en logits.
6.1.2 Medidas independientes de las personas o ítems que se usen
El modelo de Rasch utiliza el hecho de que el ordenamiento de los ítems según su dificultad es invariante con respecto a la población utilizada, al igual que el ordenamiento de las personas según su puntuación total es invariante con respecto a los ítems utilizados. Por tanto, sin importar los ítems que se utilicen el conjunto de personas evaluadas tendrá el mismo ordenamiento. Esta propiedad permite generar una medida de las habilidades y de las dificultades con la misma escala de intervalo.
Este supuesto permite establecer cuáles ítems tienen una alta probabilidad de haber sido acertados por cada sujeto, según su puntuación observada. De esta manera, una persona con 5 ítems correctos, probablemente obtuvo los 5 ítems más fáciles correctos. Los supuestos anteriores brindan elementos para examinar si la escala propuesta cumple con un conjunto de características apropiadas. Si muchos ítems o personas no presentan los patrones esperados es posible que la escala no funcione apropiadamente.
Finalmente, el ordenamiento de los ítems y las personas brinda un significado de la escala en función de los ítem que es capaz de resolver la persona.
6.1.3 Errores estándar de medida distintos según nivel de habilidad
La precisión de la estimación del nivel de habilidad está asociada a la cantidad de ítems que permiten discriminar entre los niveles de habilidad posibles para el individuo. Las personas con notas altas o bajas obtendrán errores estándar de medida altos debido a que no se cuenta con suficientes ítems que permitan determinar si deberían tener un nivel de habilidad más alto.
6.2 Fórmula
La fórmula matemática del modelo de Rasch que describe la probabilidad de acierto de un ítem \(i\) de una persona \(j\), dada la habilidad de la persona \(\theta_j\) y la dificultad del ítem (\(b_i\)), es la siguiente
\[P(X_{ij}=1|\theta_i,b_j)=\frac{e^{\theta_j-b_i}}{1+e^{\theta_j-b_i}}\]
La curva que modela la probabilidad de esa fórmula en función de \(\theta\) se denomina curva característica del ítem. Un ejemplo de esta curva, con \(b=1\), es la siguiente:
Note que la persona con habilidad igual a la dificultad del ítem posee una probabilidad de 0.5 de acierto. Por tanto, la dificultad de un ítem es el valor de habilidad en el que hay una probabilidad de 0.5 de acierto. Los niveles de la dificultad son los siguientes:
- \(]\infty, -2[\) : Muy fácil
- \([-2,-0.5[\) : Fácil
- \([-0.5, 0.5]\) : Medio
- \(]-0.5, 2]\) : Difícil
- \(]2,\infty[\) : Muy difícil (Hambleton et al, 1991)
Por otro lado, la fórmula del modelo permite estimar las probabilidades de responder un ítem para un nivel de habilidad dado, por ejemplo la probabilidad de una persona con una habilidad de 0 logits en el ítem con dificultad 1 es igual a
\[P(X_{ij}=1|\theta_i=0,b_j=1)=\frac{e^{0-1}}{1+e^{0-1}}=0.27\] Con esta información, también se puede estimar la probabilidad de fallo \(Q(\theta)=1-P(\theta)=0.73\).
6.2.1 Supuestos del modelo
Los principales supuestos del modelo son la unidimensionalidad y la independencia local. El primero es esperable en cualquier modelo de medición que trabaje con instrumentos que miden un único constructo. El segundo indica que la probabilidad de responder un ítem no es afectada por la probabilidad de responder otro ítem.
Para evaluar la independencia local se examinan los estadísticos Q3 de cada pareja de ítems, los cuales brindan el valor de la correlación de los residuos asociados a la modelación de las respuestas de los ítems. Se dice que dos ítems no son independientes si el estadístico Q3 es superior a 0.40 (Linacre).
[1] 0.23460496.3 Ejemplo de aplicación del modelo de Rasch
Para ejemplificar el uso del modelo de Rasch se va a utilizar la fórmula reducida de vocabulario. En los 12 ítems.
bTCT b ee
RC2 0.682 -1.128 0.048
RC4 0.210 1.994 0.055
RC6 0.615 -0.687 0.047
RC8 0.545 -0.257 0.046
RC9 0.491 0.078 0.046
RC12 0.701 -1.258 0.049
RC13 0.616 -0.697 0.047
RC15 0.614 -0.685 0.047
RC17 0.715 -1.355 0.050
RC18 0.244 1.723 0.053
RC19 0.184 2.232 0.058
RC20 0.497 0.040 0.046El gráfico de los primeros dos ítems es el siguiente:

6.4 Estimación de la habilidad
En el modelo de Rasch existe una única estimación de la habilidad, para cada puntuación total observada, esta habilidad se obtiene por medio de un método estadístico que permite obtener los parámetros con los que el modelo se ajusta de mejor manera a los datos.
En el caso del test de vocabulario la tabla de correspondencia de las puntuaciones totales con las habilidades, junto con sus errores estándar de medición, es la siguiente:
Person Parameters:
Raw Score Estimate Std.Error
0 -3.7721633 NA
1 -2.8627626 1.0688996
2 -2.0196696 0.8110062
3 -1.4474259 0.7140030
4 -0.9718993 0.6709538
5 -0.5338829 0.6564692
6 -0.1011756 0.6621812
7 0.3509652 0.6854445
8 0.8470074 0.7258961
9 1.4157265 0.7858317
10 2.1045560 0.8831557
11 3.0688471 1.1226980
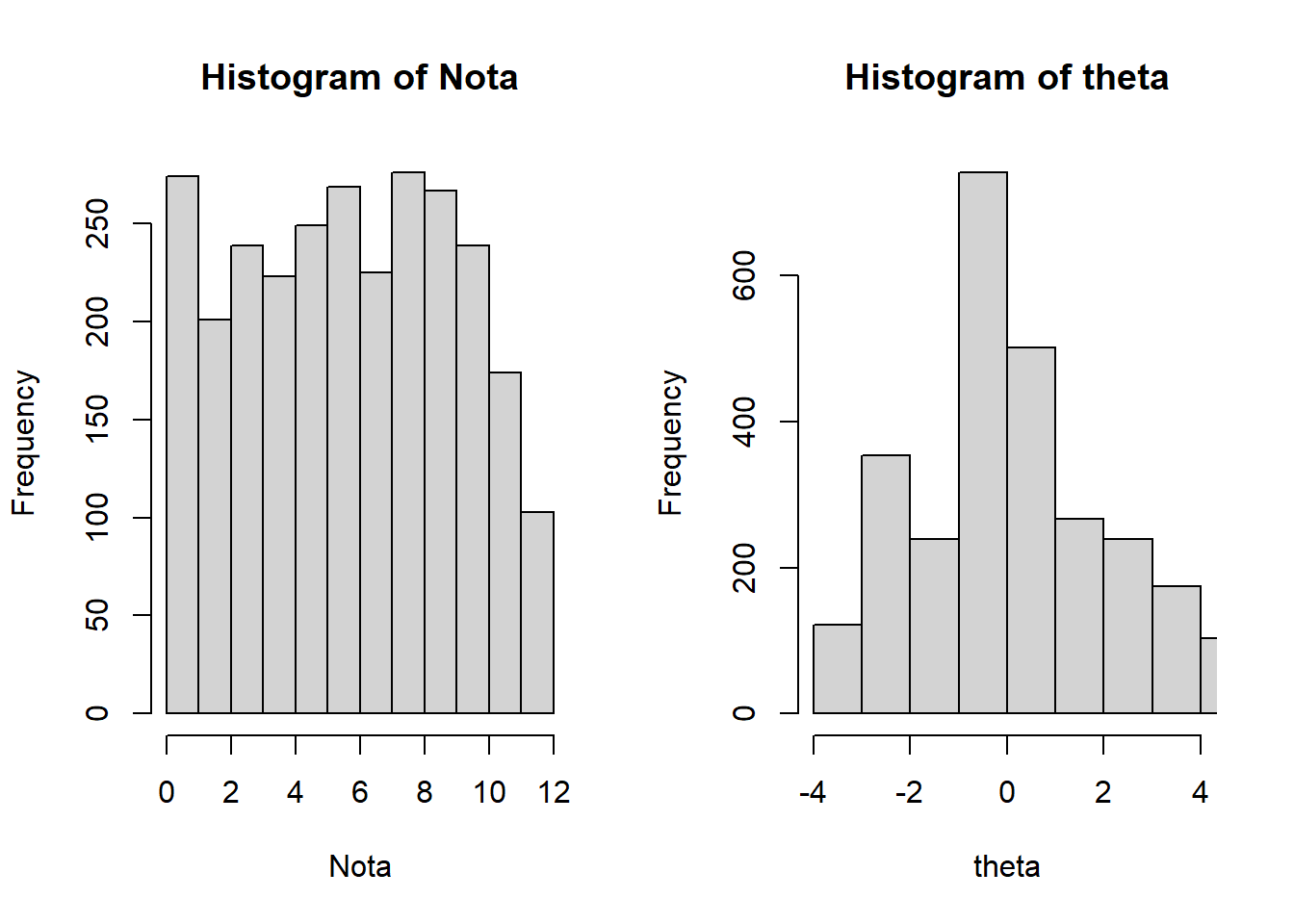
12 4.0995221 NACuando se grafican los histogramas de las puntuaciones totales observadas en la TCT y las habilidades estimadas en el modelo de Rasch se puede observar que el segundo histograma presenta una mayor tendencia a una distribución normal. En el caso del test de vocabulario los histogramas son los siguientes:
Además, en cada valor de la habilidad se estima un error estándar de medición, el cual a diferencia de lo observado en la TCT, no es igual para todas las habilidades estimadas. El valor del error estándar de medición se obtiene con la fórmula
\[\sigma_e(\theta)=\frac{1}{\sqrt{I(\theta)}}=\frac{1}{\sqrt{\sum P_i(\theta)Q_i(\theta)}}\]
El inverso del error de medición al cuadrado se denomina función de información. Esta función indica en cuáles valores de la habilidad se obtienen las estimaciones más precisas del test. Un valor de la curva de información superior a 16 indica una precisión bastante alta, ya que el error de medición sería de apenas .25 unidades. En el gráfico adjunto se presenta la función de información del test:
plotINFO(mod, type="test")6.4.1 Intervalo de confianza
El intervalo de confiana de la habilidad estimada para los individuos puede calcularse con la fórmula \(\theta\pm Z_{1-\alpha/2}\sigma_e\), donde \(\sigma_e\) corresponde al error estándar de medición, el cual varía en función de las habilidades estimadas.
En el ejemplo del test de voacabulario, en el caso de una persona con habilidad \(\theta=-2.86\) y \(eem=-1.07\), el intervalo de confianza del 95% es
\[-2.86\pm 1.96\cdot -1.07 = ]-4.96,-0.77[\] Nótese que este intervalo es bastante amplio, pero para una persona con habilidad de \(\theta=-0.53\), el error estándar de medida es 0.66, que es casi la mitad del error estándar del caso previo. En este caso el intervalo de confianza del 95% de la habilidad es \(]-1.82, 0.75[\).
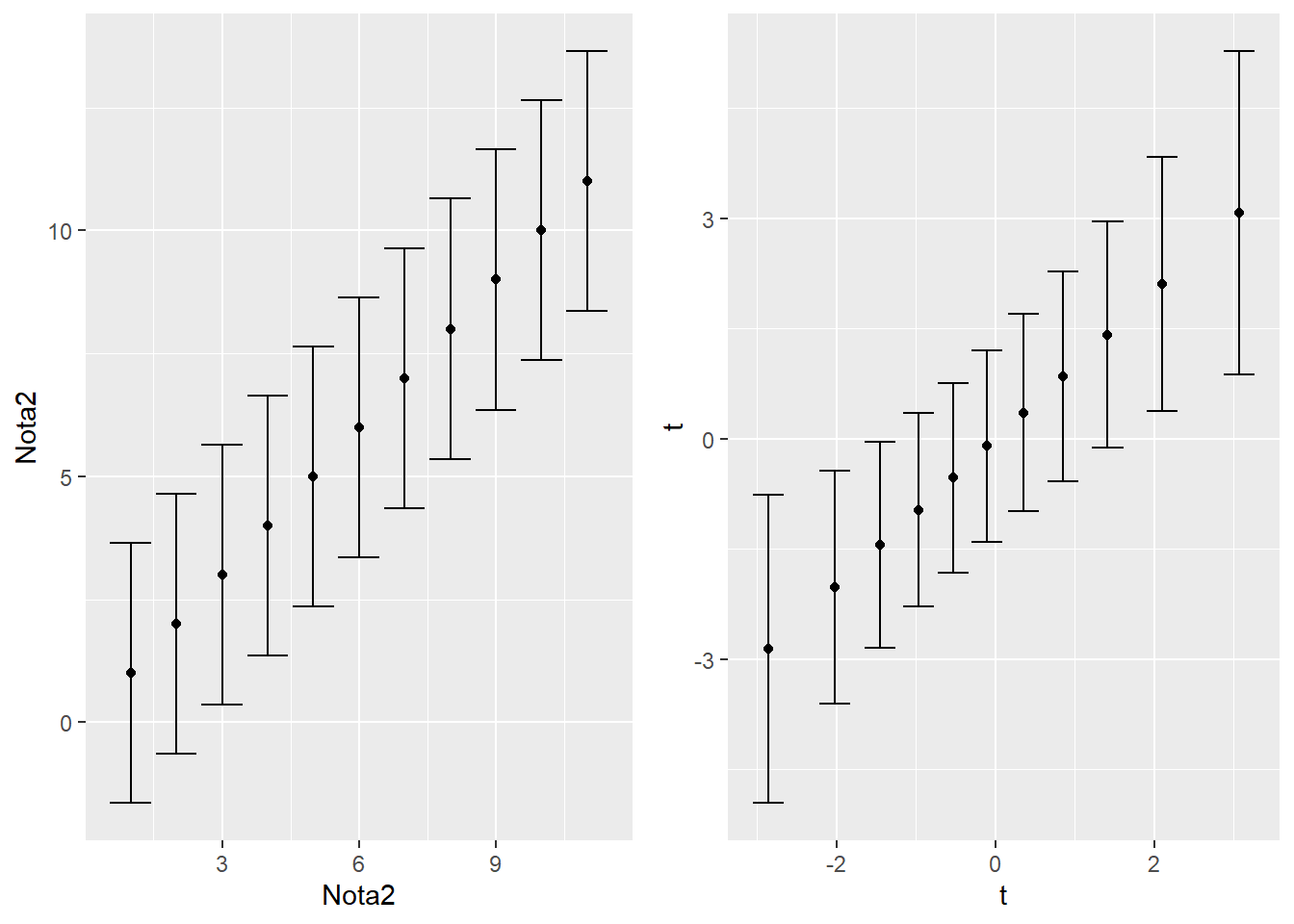
Por último, nótese cómo varían los intervalos de confianza dentro del modelo de Rasch, en comparación con la TCT.
6.4.2 Mapa de ítems-personas
En la formulación del modelo de Rasch, las habilidades de las personas y las dificultades de los ítems se estiman en la misma escala. Esta propiedad permite graficar estos parámetros en una misma gráfico y poder observar cuáles ítems tienen alta probabilidad de ser resueltos por un grupo de examinados (\(p>.50\)). El gráfico de ítems-personas del test de vocabulario es el siguiente:
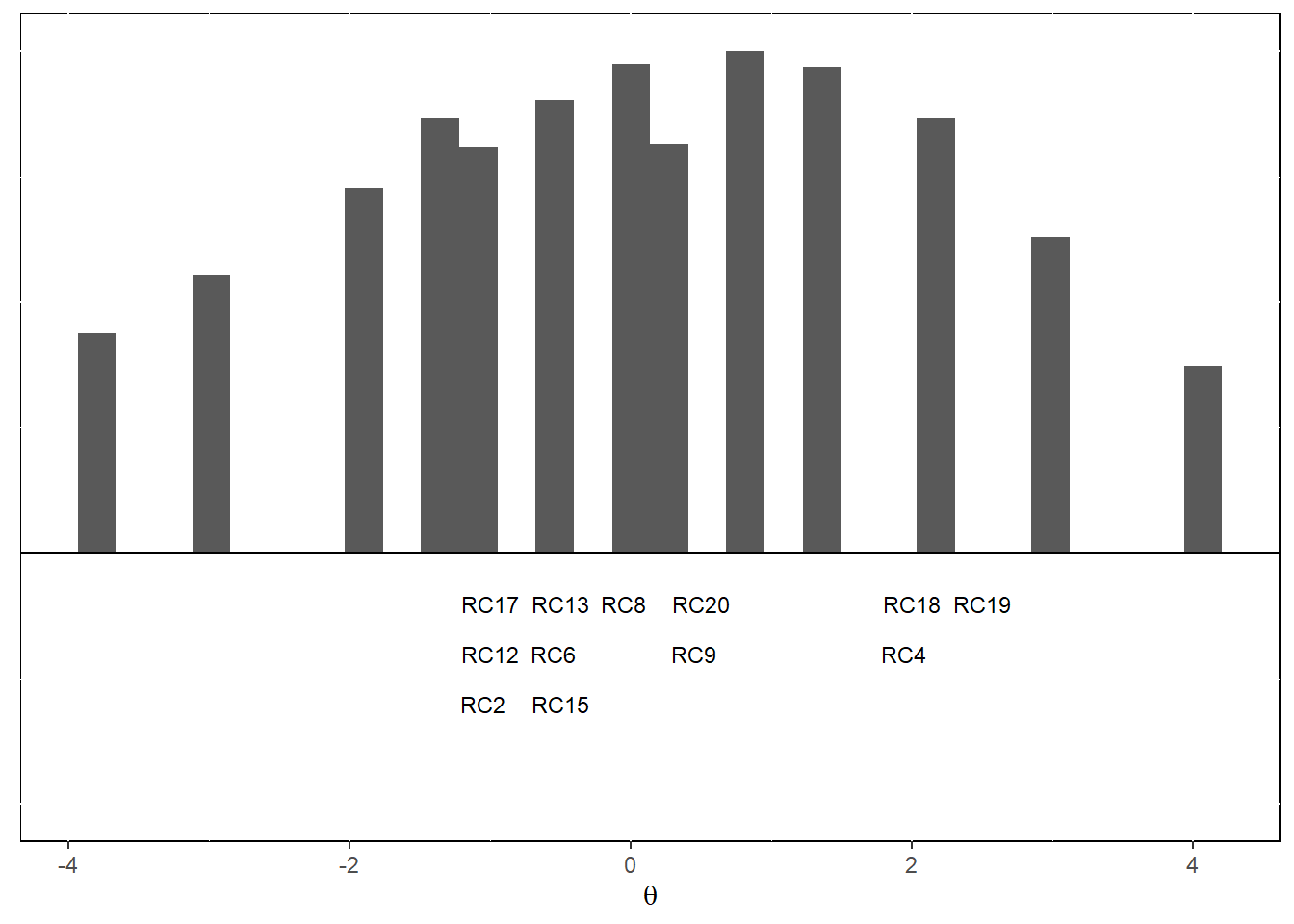
En el gráfico se puede observar que hay varios grupos de personas que no tienen la habilidad suficientes para responder correctamente todos los ítems. Por otro lado, se puede ver que las personas con un nivel de habilidad de 1 pueden resolver 9 ítems correctamente, pero 3 no.
6.5 Ajuste del modelo
Existen varios índices que permiten evaluar el ajuste de los ítems y las personas al modelo de Rasch. El coeficiente infit MSQ señala patrones inesperados de respuestas, como repuestas incorrectas de las personas para las cuales los ítems están diseñados. El outfit MSQ señala patrones con respuestas correctas inesperadas, lo cual puede ser derivado del azar. Los coeficientes infit y outfit mayores a 2 indican problemas de ajuste de los ítems.
Cuando se presentan persona o ítems que no ajustan al modelo se pueden eliminar de la base de datos, para volver a estimar el modelo y obtener coeficientes más confiables. Esta es una decisión que debe ser claramente justificada.
En el caso del test de vocabulario se obtuvieron los siguientes valores de infit MSQ y outfit MSQ:
outfitMSQ infitMSQ
RC2 1.0764276 1.0865182
RC4 1.1631104 1.1234735
RC6 0.9628500 1.0345188
RC8 0.7590495 0.8543401
RC9 0.7940039 0.8797156
RC12 0.8691573 0.9251546
RC13 0.7939826 0.9000921
RC15 1.2131925 1.1866643
RC17 0.8798687 0.9422951
RC18 0.8308434 0.9380916
RC19 0.7465545 0.8482042
RC20 0.7660805 0.8498880Se puede observar que no se presentó ningún ítem con problemas en el infit o en el outfit.
Por otro lado, también se puede analizar el ajuste de las personas la modelo, por medio de los mimos indicadores. En este análisis se puede aumentar el valor del punto de corte a 4, para solamente centrarse en los casos realmente problemáticos. Los valores del outfit superiores a 4 observados en el test fueron los siguientes:
4185 9481 595 10093 4247 727 3993 9849
10.817098 10.817098 7.059415 7.059415 6.715586 6.413019 6.413019 6.367405
12001 692 8919 1054 10060 5539 10279
6.367405 6.241982 5.642939 4.954033 4.318249 4.027194 4.027194 El patrón de respuestas, en los ítems ordenados según dificultad, de la persona con el outfit más grande fue el siguiente:
RC17 RC12 RC2 RC13 RC6 RC15 RC8 RC20 RC9 RC18 RC4 RC19
4185 0 0 0 0 0 0 0 0 0 0 1 0Se puede observar que el outfit detectó un patrón con una pregunta respondida correctamente, de forma inesperada. La persona con una única respuesta correcta posee una habilidad insuficiente para responder algún ítem de la prueba, en especial es claramante insuficiente para responder el degundo ítem más difícil.
Por otro lado, los valores de los infit de las personas fueron los siguientes:
9803 11838 555 4888 4724 3792 7280 2752
2.403993 2.347117 2.330567 2.240789 2.170763 2.110416 2.106896 2.084432
3158 10854 9782 11403 9790 7690 2062 5464
2.056182 2.052524 2.008757 1.995136 1.985555 1.984136 1.975599 1.954299
5653 3032 340 3914
1.953607 1.933604 1.919088 1.896491 Ninguno de los infit mostró un valor extremo.
Finalmente, se puede presentar un índice del ajuste total del modelo a los datos. El SRMSR (standardized root mean square root of squared residuals, Maydeu-Olivaras, 2013) compara las correlaciones observadas de los residuos de los ítems con los valores estimados por el modelo. Se espera que este índice sea menor a 0.08. En el caso del ejmeplo de vocabulario el valor fue
SRMSR
0.05385357 6.6 Sintaxis con R
Cargar la base de datos
BASE<-read.csv("Vocab1.csv",sep=",")Seleccionar el conjunto de ítems
BASE<-subset(BASE,engnat==2)
num<-c(82, 84, 86, 88, 89, 92, 93, 95, 97, 98, 99, 100)
ITEMS<-BASE[,num]
rownames(ITEMS)<-1:dim(ITEMS)[1]Comprobar supuesto de independencia local
library(TAM)
fit0 <- tam(ITEMS)
Res0 <- tam.modelfit(fit0)
Q3 <- Res0$Q3.matr
max( abs(Q3) , na.rm=T )
round( Q3, 2)Estimar el modelo
library(eRm)
fit<- RM(ITEMS)Ver los coeficientes de los ítems
Res<-data.frame(-fit$beta,fit$se.beta)
ResVer las habilidades de las personas
pp<-person.parameter(fit)
ppGraficar una curva característica del ítem
plotICC(fit, 1) ##SELECCIONAR CURVA DE INTERÉSGráficar varias curvas características del ítem
plotjointICC(fit, item.subset = c(1,2), legpos = "left") ##SELECCIONAR CURVA DE INTERÉSGraficar la función de información
plotINFO(fit, type="test")Graficar el mapa de item-personas
plotPImap(fit)Evaluar el infit y el outfit de los ítems
itemsfit<-itemfit(pp)
itemsfitGenerar el infit y el outfit de las personas
infitp<-personfit(pp)$p.infitMSQ
outfitp<-personfit(pp)$p.outfitMSQVer la población con outfit>4
outfit4<-outfitp[outfitp>3.99]
outfit4Crear una base sin individuos con outfit>4
id<-as.numeric(names(outfitp[outfitp>3.99]))
ITEMS2<-ITEMS[-id,]Evaluar el ajuste global del modelo
#library(TAM)
#fit0 <- tam(ITEMS)
#Res0 <- tam.modelfit(fit0)
Res0$fitstat[3]6.7 Guía de trabajo
Utilice los ítems 2, 4, 6, 8, 9, 12, 13, 15, 17, 18, 19 y 20 de la base vocabulario, sin delimitar a población hablante nativa, para contestar las siguientes preguntas.
Justifique si la base de datos cumple los supuestos del modelo de Rasch (2 puntos).
Estime las dificultades de los ítems (1 punto).
Para el ítem más difícil de la base de datos realice los siguientes análisis:
- Presente su curva característica del ítem (1 punto).
- Determine las probabilidades de acierto de una persona con una habilidad de 0 logits y otra con una habilidad de 1 logit (2 puntos).
- Presente el infit y el outfit del ítem. Indique si el ítem presenta algún problema de ajuste al modelo (2 puntos).
Encuentre la persona con el outfit más grande de la base y explique por qué posee ese valor (2 puntos).
Calcule el intervalo de confianza de la habilidad para una persona con 6 preguntas correctas (1 punto).
Presente el mapa de items-personas e indique dos conclusiones que se pueden hacer de este mapa (3 puntos).
6.8 Referencias
Hambleton, R. K., Swaminathan, H., & Rogers, H. J. (1991). Fundamentals of item response theory. Sage Publications, Inc.
https://scholarworks.umass.edu/cgi/viewcontent.cgi?article=1470&context=pare