H M
1 6.50846 5.737435 Impacto, sesgo y funcionamiento diferencial
5.1 Impacto
Las diferencias observadas en las notas de un test entre dos grupos de población se denomina impacto. Estas diferencias son esperadas en los test, debido a las distintas oprtunidades de los grupo de población aplicantes de la prueba. Por ejemplo, un test de lenguaje inglés entre personas nativas del idioma y no nativas presentará un nivel alto de impacto. En cambio, al comparar por géneros no se esperarían diferencias muy grnades. En el caso del test de vocabulario estudiado, se observaron los siguientes promedios según género:
Un indicador que permite determinar el tamaño del efecto en las diferencias de promedios es la d de Cohen, cuya fórmula es
\[d=\frac{\overline{X_1}-\overline{X_2}}{s_p}\]
con \(s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_1^2}{n_1+n_2-2}}\). Este tamaño se considera pequeño si está entre 0.2 y 0.5, mediano si está entre 0.5 y 0.8 y, grande si su valor es mayor a 0.8
En el caso del test de vocabulario, el tamaño del efecto fue igual a:
[1] -0.12643715.2 Sesgo
Desde el enfoque de la justicia (fairness), el sesgo hace referencia a elementos del diseño o la logística del test que afectan el desempeño de un grupo. Entre estas amenazas está la subsestimación de las puntuaciones en los test debido a falta de atención a necesidades de grupos, como adecuaciones de acceso. Otra caso de sesgo se puede observar en test que requieren interacción con los calificadores, ya que estos pueden extrapolar sus tendencias hacia algún grupo.
Desde el enfoque de la medición, el sesgo es un error sistemático en el cálculo de las puntuaciones de un test, que afecta a un grupo en particular (AERA et al., 2014, Martínez, 2007). El grupo potencialmente perjudicado se le denomina grupo focal, mientras que al grupo de comparación se le llama grupo de referencia. Desde el enfoque de la medición, el sesgo se divide en externo e interno.
El sesgo externo o predictivo refiere a diferencias en la predicción de un criterio externo entre grupos, esto se ve cuando la recta de predicción de la variable criterio, en función de la nota del test, es distinta en los grupos de interés (Aguinis, Pierce y Culpepper, 2010).
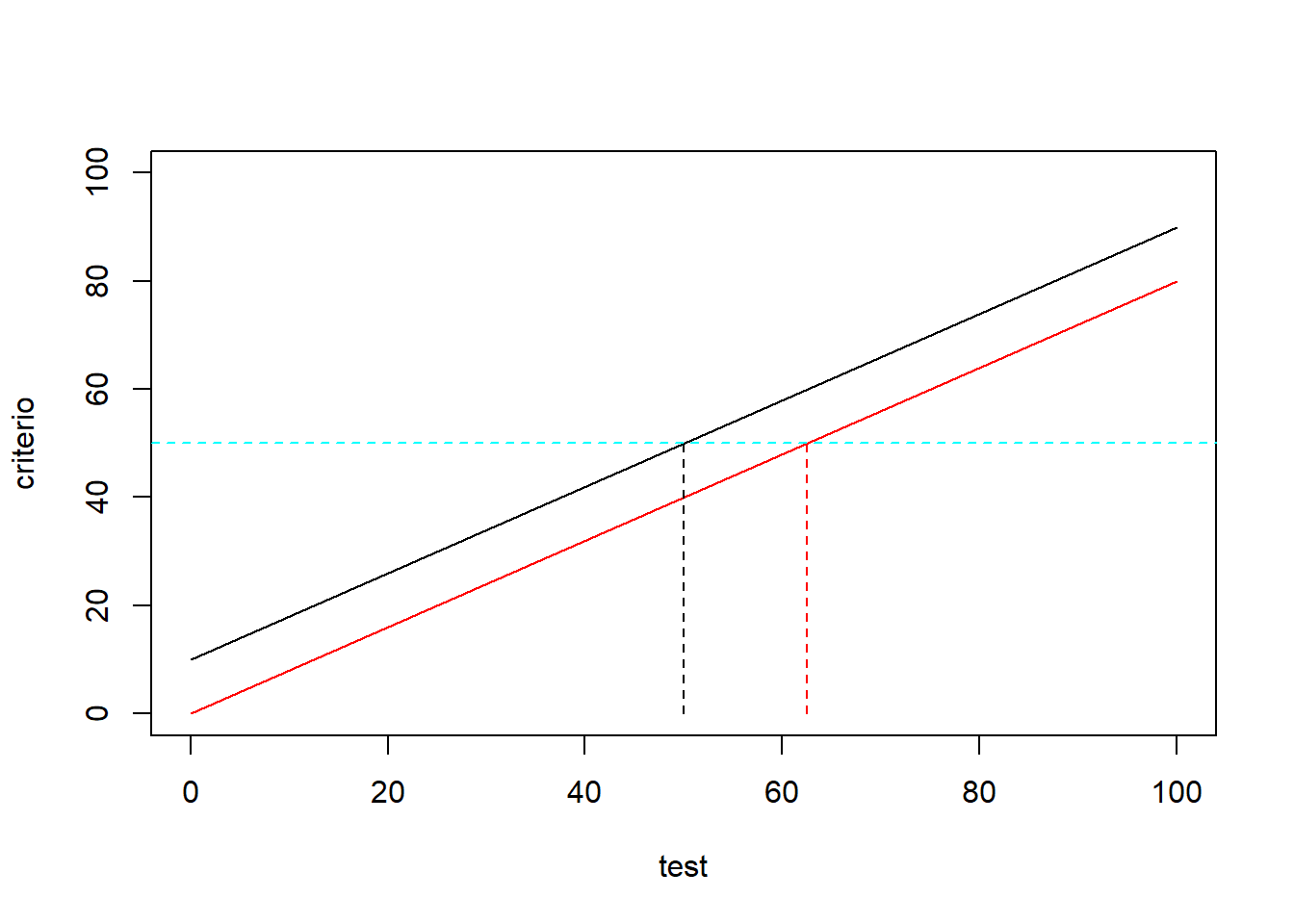
En el ejemplo adjunto, las personas con una nota de 50 en el grupo negro, presentan igual rendimiento criterio que aquellas con un 65 en el grupo rojo; por tanto, las personas del grupo rojo pudieron tener una sobreestimación de la puntuación. El fenómeno ocurrido al grupo rojo se denomina sobrepredicción y se da cuando la curva de regresión posee un intercepto menor que la curva del otro grupo. La sobrepredicción de notas de grupos minoritarios es el sesgo externo más reportado en la literatura (Aguinis, Pierce y Culpepper, 2010).
El sesgo interno se refiere a las diferencias en las propiedades de medición internas del test. La forma más utilizada para empezar la detección de este sesgo es el Funcionamiento Diferencial del Ítem (DIF). Luego de este procedimiento, se recomienda realizar estudios con grupos pequeños para confirmar la presencia de diferencias.
Es importante notar que el sesgo desde el enfoque de medición y desde el enfoque de la justicia no presentan implicaciones entre ellas. Por tanto, un ítem con sesgo de medición no indica la presencia de elementos de desventaja para algún grupo particular, que es la forma más común de definición de sesgo.
5.3 Funcionamiento Diferencial del Ítem
El DIF refiere a la “diferencia en el desempeño en un ítem de dos grupos comparables de examinados, es decir, que han sido enlazados con respecto al constructo medido en el test” (Dorans y Holland, 2005). El DIF refleja una diferencia inesperada entre los grupos poblacionales, dado que las habilidades de sus integrantes son controladas.
5.3.1 Método de Mantel -Haenszel
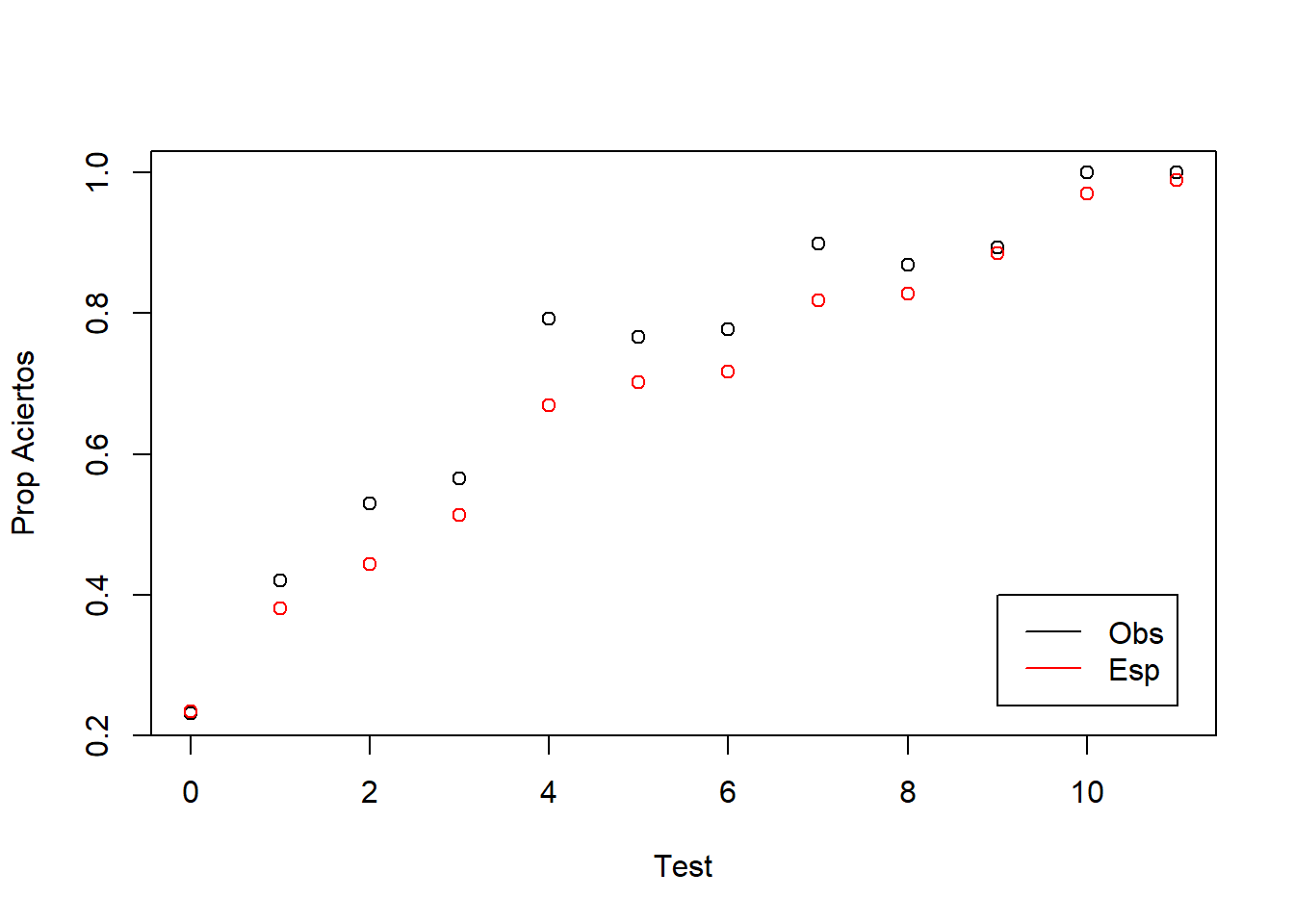
En este método se estudia si la probabilidad de acierto de un ítem, controlando el nivel de habilidad, es igual entre grupos. Para esto se comparan la cantidad de personas que acertaron el ítem del grupo de referencia con la cantidad esperada, controlando el nivel de habilidad. En el caso del test de vocabulario de 12 ítems se tienen las siguientes proporciones observadas y esperadas, para el primer ítem:
5.3.1.1 Fórmula
El estadístico de análisis de la prueba Mantel-Haenszel utiliza la siguiente notación para la tabla de contingencia de los grupos versus el acierto, según nivel de habilidad \(j\),
| 1 | 0 | ||
|---|---|---|---|
| Ref | \(A_j\) | \(B_j\) | \(N_{R.j}\) |
| Focal | \(C_j\) | \(D_j\) | \(N_{F.j}\) |
| \(N_{.1j}\) | \(N_{.0j}\) | \(N_{..j}\) |
y su fórmula es la siguiente
\[\chi^2= \frac{\left(|\sum A_j- \sum E(A_j)|-0.5\right)^2}{\sum Var(A_j)}\] con \(E(A_j)=\frac{N_{R.j}N_{.1j}}{N_{..j}}\) y \(Var(A_j)=\frac{N_{R.j}N_{F.j}N_{.1j}N_{0.j}}{N_{..j}^2(N_{..j}-1)}\)
Ahora bien, para determinar si un ítem posee DIF se realiza una prueba de hipótesis con un grado de libertad (Guilera, Gómez-Benito, Hidalgo y Sánchez-Meca, 2007).
Finalmente, se puede determianr si el tamaño del DIF es grande por medio del estudio del índice \(\Delta_{MH}\). Si este es mayor o igual que 1.5 se dice que el tamaño del efecto es grande (Holland and Thayer, 1985).
5.3.1.2 Ejemplo
Los estadísticos observados en los 12 ítems del test de vocabulario son los siguientes:
item MH p Delta
1 RC2 29.06796371 0.000 1.304
2 RC4 0.05089041 0.822 0.074
3 RC6 1.29175647 0.256 0.278
4 RC8 3.19447951 0.074 0.464
5 RC9 5.12929554 0.024 0.572
6 RC12 0.21463948 0.643 0.134
7 RC13 33.73009955 0.000 1.500
8 RC15 17.40350217 0.000 0.930
9 RC17 0.28595955 0.593 0.154
10 RC18 2.63876280 0.104 0.454
11 RC19 15.89562868 0.000 1.292
12 RC20 0.73729361 0.391 0.229Nótese que el primer ítem de la prueba, estudiado previamiente, presenta un estadístico chi significativo, por lo cual se concluye que este presenta un funcionamiento diferencial del ítem. No obstante, su tamaño del efecto es menor que 1.5, por lo cual no se considera que implique diferencias grandes.
5.4 Sintaxis en R
Cargar la base
BASE<-read.csv("Vocab1.csv",sep=",")
BASE<-subset(BASE,engnat==2)Seleccionar el conjunto de ítems codificado en correcto/incorrecto
ITEMS<-BASE[,c(82, 84, 86, 88, 89, 92, 93, 95, 97:100)]Seleccionar las variables auxiliares: variable de grupo y Nota
gen<-BASE$gender
gen[gen==0]<-NA
gen[gen==3]<-NA
Nota<-rowSums(ITEMS)Diferencia de medias entre grupos (previa verificación del supuesto de homoscedasticidad)
bartlett.test(Nota ~ gen)
t.test(Nota ~ gen )Tamaño del efecto de la diferencia
#install.packages("effsize")
library(effsize)
cohen.d(Nota ~ gen)Diferencias de proporciones en los ítems
x<-table(ITEMS[,1], gen)[2,] #INDICAR LA POSICIÓN DEL ÍTEM DE INTERÉS
n<-table(gen)
prop.test(x, n) Coeficiente h de Cohen
p<- x / n
h<-2*(asin(p[1])-asin(p[2]))
hMétodo Maentel Haenszel de DIF
library(difR)
MH<-difMH(data.frame(ITEMS,gen), group = "gen", focal.name = 2)
ES<- abs(-2.35*log(MH$alphaMH))
ResMH<-data.frame(MH$names,MH$MH,round(MH$p.value,3),round(ES,3) )
names(ResMH)<-c("item","MH","p", "Delta")
ResMH5.5 Guía de trabajo
Utilice los ítems 2, 4, 6, 8, 9, 12, 13, 15, 17, 18, 19 y 20 de la base vocabulario, sin delimitar a población hablante nativa, para contestar las siguientes preguntas.
Determine si existen evidencias para concluir que el test presenta un impacto considerable entre hablantes nativos y no nativos.
Determine el ítem con el tamaño del efecto de diferencias de proporciones más alto, entre hablantes nativos y no nativos.
Determine los ítems con DIF Maentel Haenszel, según la prueba de hipótesis, entre hablantes nativos y no nativos.
Determine los ítems con DIF Maentel Haenszel, según el tamaño del efecto, entre hablantes nativos y no nativos.