7 Teoría de Respuesta al Ítem
7.1 Descripción de la Teoría de Respuesta al Ítem
La Teoría de Respuesta al Ítem (TRI) es un modelo de medición de variables latentes que estima la habilidad de los individuos en función de los ítems particulares contestados correctamente. Para el estudio de las propiedades de los ítems y las personas utiliza una fórmula para cada ítem, en la que modela la probabilidad de respuesta del ítem en función de la habilidad de las personas y los parámetros de los ítems.
Al igual que el modelo de Rasch a) usa una escala distinta a la TCT (logits normalizados) y b) no asume que el test es igual de preciso para todo los niveles de habilidad. A diferencia del modelo de Rasch a) no asume que los ítems contribuyen por igual a la estimación de la habilidad y b) no asume que los ítems presentan el mismo ordenamiento para todas las personas.
Por otro lado, en la TRI se busca el valor de los parámetros que permitan maximizar el ajuste del modelo a los datos.
7.1.1 Los ítems tienen distintos pesos en la estimación de la habilidad
En el modelo de Rasch y en la TCT todos los ítems presentan la misma contribución a la estimación de la habilidad. En el caso de la TRI, se postula que algunos ítems presentan mayores contibuciones a la evaluación, que otros reactivos.
7.1.2 El ordenamiento de los ítems no es igual para todos los individuos
En el modelo de Rasch se asumía que el ordenamiento según dificultad de los ítems era igual para todos los individuos. En la TRI este ordenamiento puede variar según niveles de habilidad de los individuos. En particular, los ítems que menos contribuyen a la evaluación son los más influyentes en los cambios de posición, para individuos con distintos niveles de habilidad.
7.1.3 Diferentes estimaciones de habilidad para puntuaciones totales iguales
En el modelo de Rasch las personas con puntuaciones totales iguales recibían la misma estimación de habilidad. En la Teoría de Respuesta al Ítem las estimaciones de habilidad dependen de los ítems contestados correctamente.
En el modelo de Rasch se asume que la habilidad es independiente de los ítems contestados correctamente, en cambio, en la TRI no se puede hacer está asunción debido a que la puntuación total no es un estadístico suficiente para la estimación de la habilidad, es decir, que para la estimación de la habilidad se requiere conocer cuales ítems fueron contestados correctamente.
7.2 Modelo de 1 parámetro
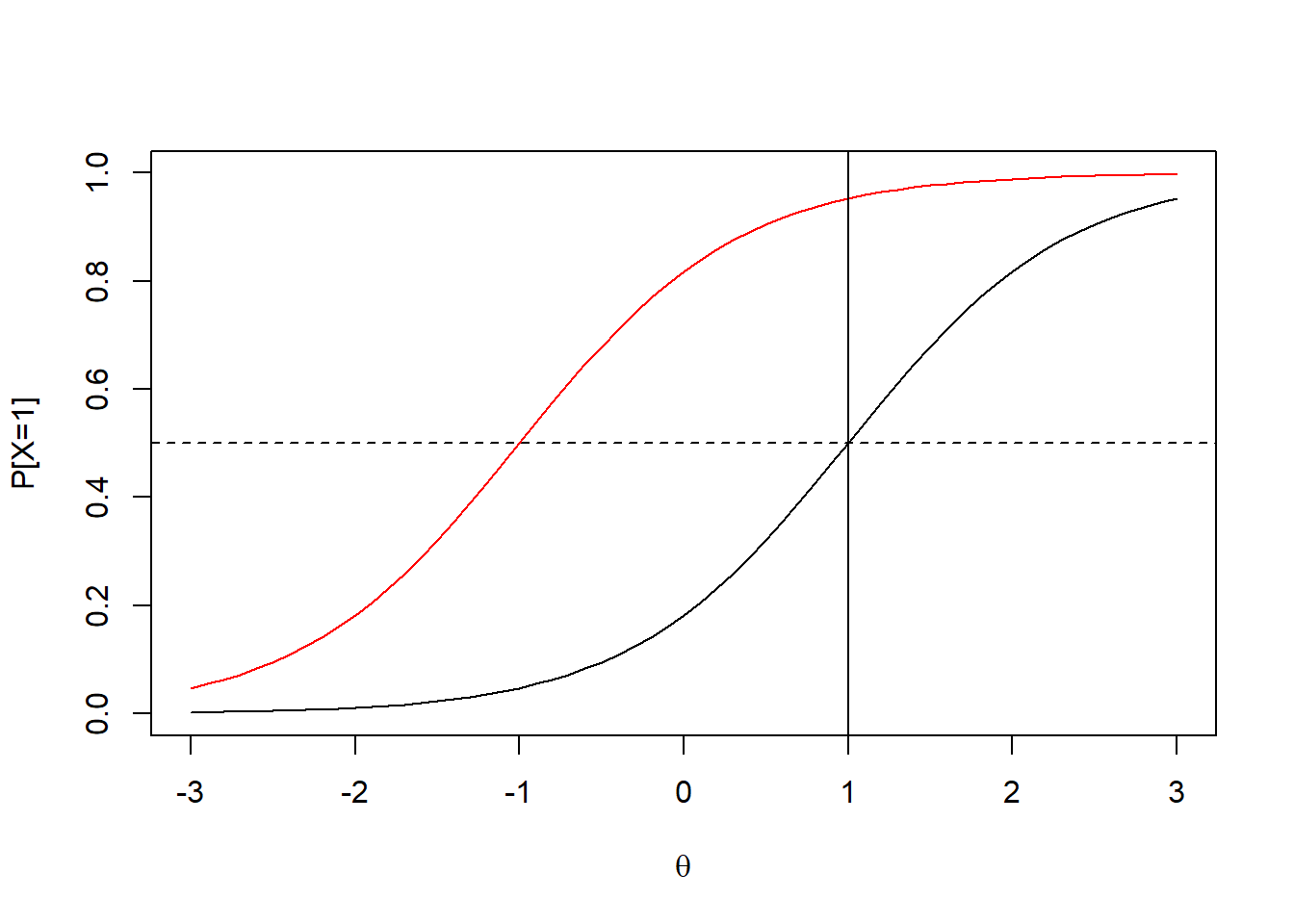
El Modelo de 1 parámetro reproduce las propiedades del modelo de Rasch, con el elemento adicional de que este modelo brinda una estimación de qué tan bien discriminan los ítems utilizados. Este modelo presenta la misma fórmula que el modelo de Rasch, con la adición de un parámetro \(a\) que indica el grado de separación entre las personas de baja habilidad y alta habilidad, en \(\theta=b_i\) para cada uno de los ítems. La fórmula de este modelo es la siguiente:
\[P(X_{ij}=1|\theta_j,a, b_i)=\frac{e^{a(\theta_j-b_i)}}{1+e^{a(\theta_j-b_i)}}\]
El parámetro de discriminación indica el cambio en la probabilidad cerca del punto \(b_i\) (valor de la pendiente de la recta tangente en \(\theta=b_i\), el cual es \(a/4\)). Aproximadamente, de \(\theta=b_i-0.25\) a \(\theta=b_i+0.25\) se observa un aumento \(a/8\) en la probabilidad. En el modelo de Rasch, que \(a=1\), se observa un aumento de .125 unidades de probabilidad.
Los niveles de discriminación son los siguientes:
- \(]0, 0.35]\): Muy baja
- \(]0.35, 0.65]\): Baja
- \(]0.65, 1.35]\): Moderada
- \(]1.35, 1.70]\): Alta
- \(]1.70, \infty[\): Muy alta (Baker, 2001)
En el gráfico adjunto se presentan dos ítems derivados del modelo, con con \(a=1.5\) y, discriminaciones \(b_1=-1\) y \(b_2=1\) , es la siguiente:
7.3 Modelo de 2 parámetros
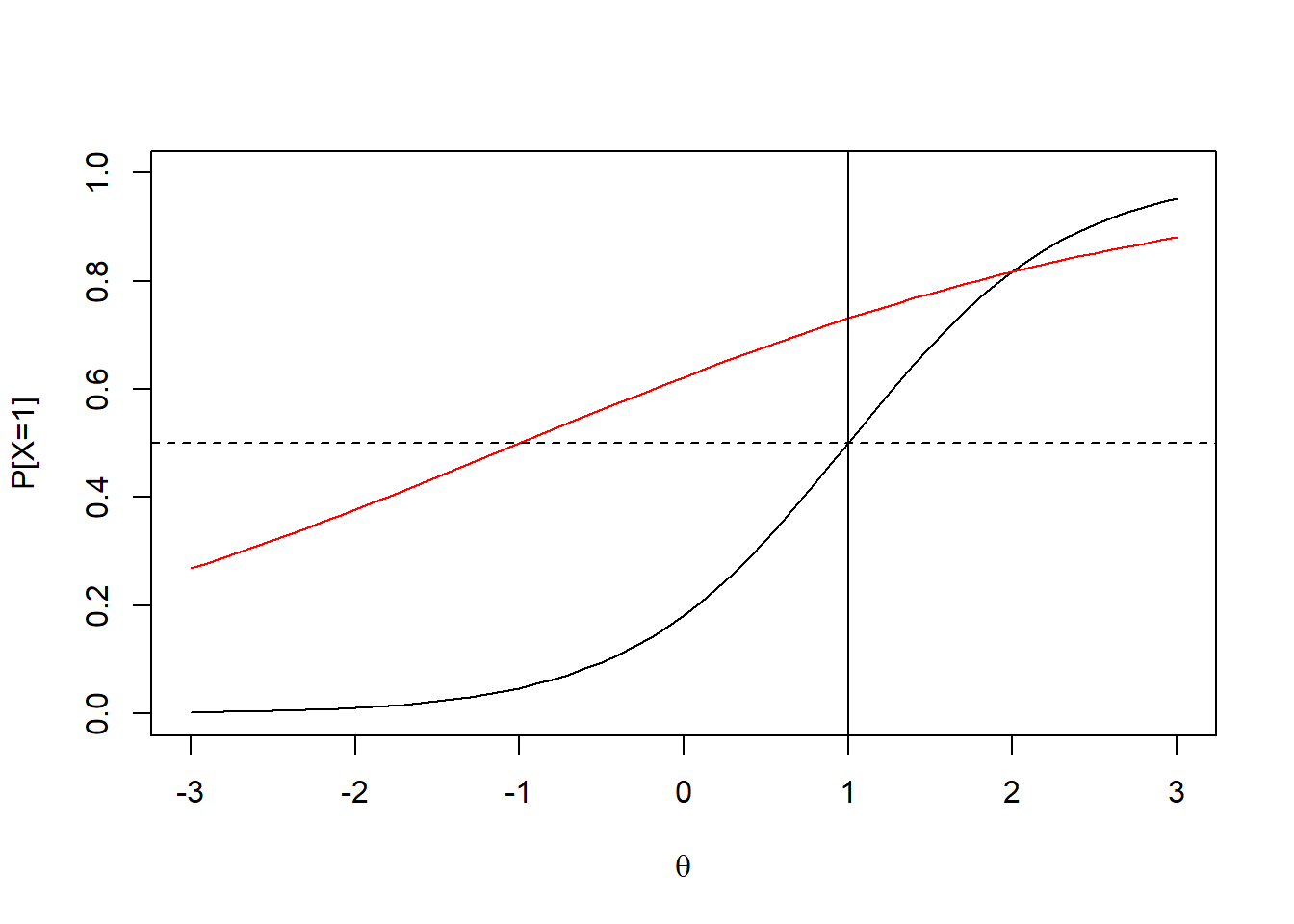
Este modelo de TRI incorpora la particularidad de estimar un parámetro de discriminación de cada uno de los ítems. La fórmula matemática de la Teoría de Respuesta al Ítem que describe la probabilidad de acierto de un ítem \(i\) de una persona \(j\), dada la habilidad de la persona \(\theta_j\) y la discriminación y dificultad del ítem (\(a_i\) y \(b_i\)), es la siguiente
\[P(X_{ij}=1|\theta_j,b_i)=\frac{e^{a_i(\theta_j-b_i)}}{1+e^{a_i(\theta_j-b_i)}}\]
En el gráfico adjunto se presentan dos ítems derivados del modelo, con con \(a_1=0.5\) y \(a_2=1.5\), discriminaciones \(b_1=-1\) y \(b_2=1\) , es la siguiente:
7.3.1 Supuestos del modelo
Al igual que en el modelo de Rasch, los principales supuestos del modelo son la unidimensionalidad y la independencia local.
7.3.2 Ejemplo de aplicación de los modelos de la Teoría de Respuesta al Ítem
Para ejemplificar el uso de los modelos de 1 y 2 parámetros se va a utilizar el conjunto de ítems de Estadística de la base de conocimientos de Estadística y Probabilidad. Los coeficientes obtenidos en el modelo de 1 parámetro (1p) y de 2 parámetros (2p) fueron los siguientes:
b_1p a_1p b_2p a_2p
D2 -2.32 1.42 -2.10 1.70
D3 -0.03 1.42 -0.04 1.05
D4 -2.87 1.42 -2.41 1.95
D5 -0.45 1.42 -0.49 1.24
D6 -1.02 1.42 -0.92 1.76
D7 -0.40 1.42 -0.43 1.30
D8 -1.20 1.42 -1.09 1.727.3.3 Estimación de la habilidad
En el modelo de 2 parámetros hay distintas estimaciones de habilidades para los individuos, en función de los ítems contestados correctamente, independientemente de si el total de respuestas es igual. A continuación se presentan los patrones de respuestas de 5 personas que tomaron el test de Estadística y presentaron 3 ítems correctos, junto con su nivel estimado de habilidad en el modelo de 2 parámetros.
D2 D3 D4 D5 D6 D7 D8 hab eem
6 1 0 1 0 0 0 1 -0.95 0.5
21 1 0 1 1 0 0 0 -1.07 0.5
24 1 0 1 0 0 1 0 -1.06 0.5
61 1 0 1 0 0 0 1 -0.95 0.5
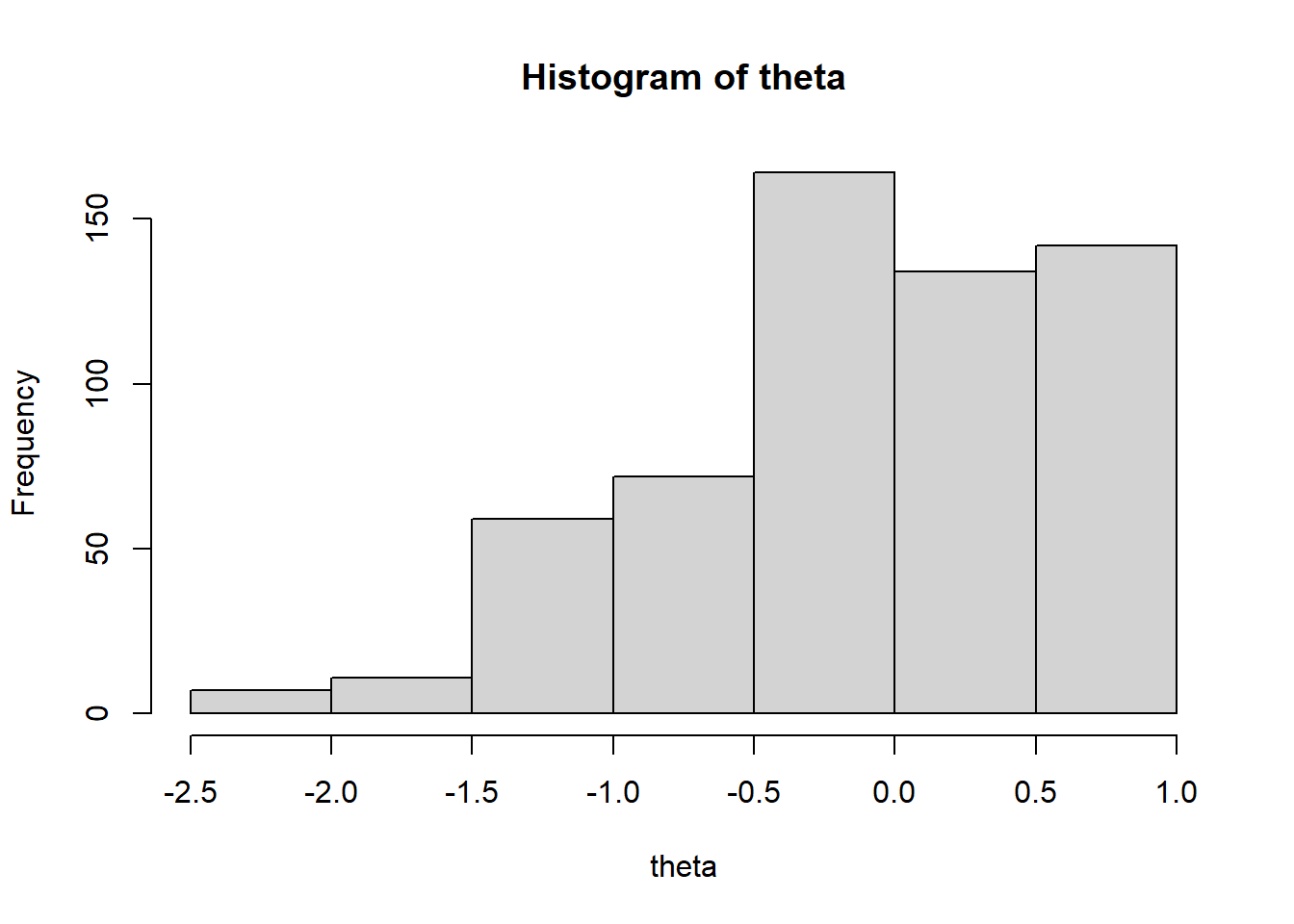
70 1 1 1 0 0 0 0 -1.12 0.5El histograma de las habilidades estimadas en dicho test, con el modelo de 2 parámetros, fueron las siguientes:
7.3.4 Intervalo de confianza
El intervalo de confianza de la habilidad estimada para los individuos puede calcularse con la fórmula \(\theta\pm Z_{1-\alpha/2}\sigma_e\), donde \(\sigma_e\) corresponde al error estándar de medición, el cual varía en función de las habilidades estimadas. El error estándar de medición en la TRI presenta la siguiente fórmula:
\[\sigma_e(\theta)=\frac{1}{\sqrt{I(\theta)}}=\frac{1}{\sqrt{\sum a_i^2P_i(\theta)Q_i(\theta)}}\]
En el ejemplo del test de Estadística, en el caso de una persona con habilidad \(\theta=-0.36\) y \(\sigma_e=0.64\), el intervalo de confianza del 95% es
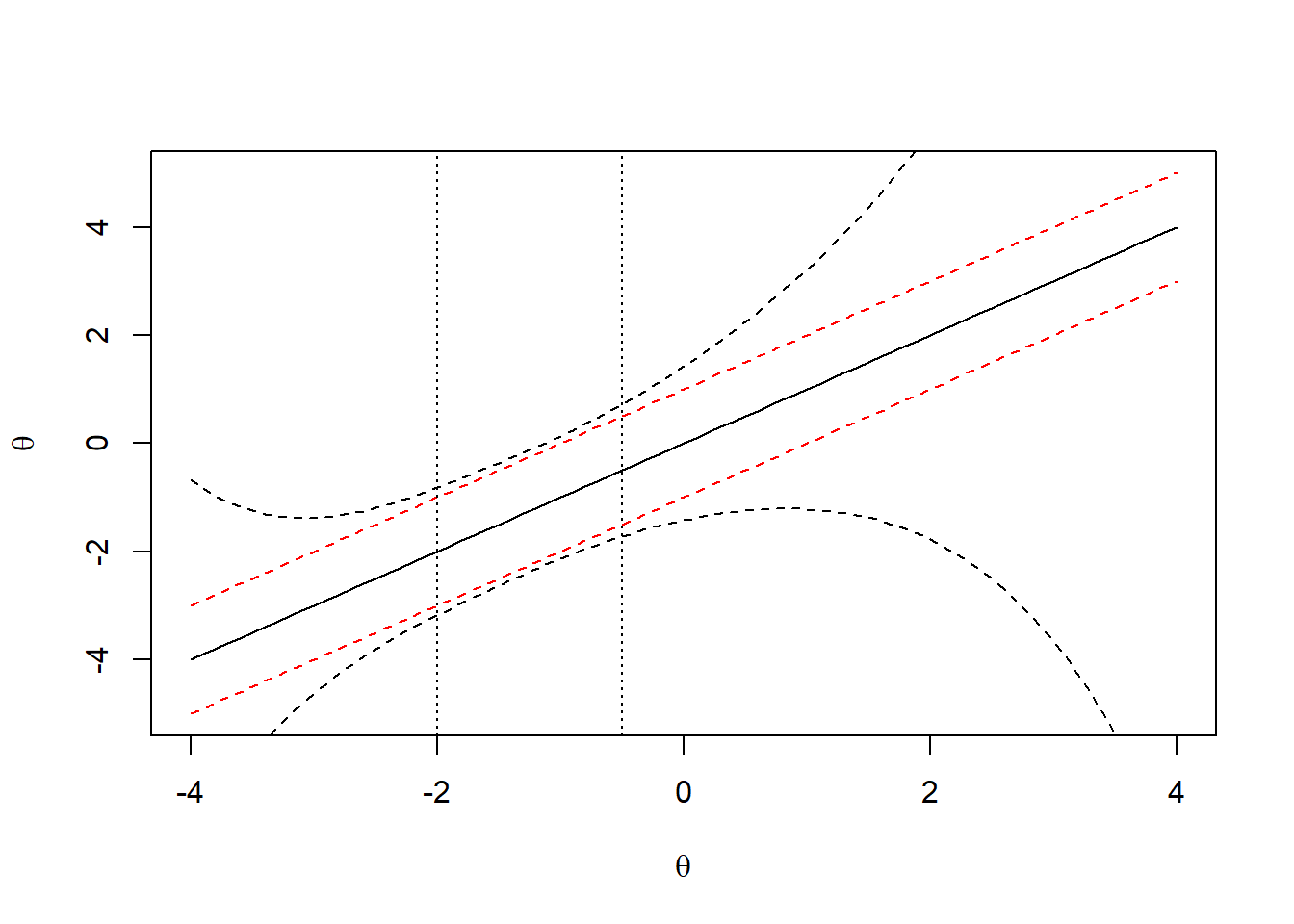
\[0.36\pm 1.96\cdot 0.64 = ]-0.89,1.61[\] Nótese que este intervalo presenta una amplitud muy amplia en la escala logit, ya que su radio es de 1.25 unidades. Los intervalos de confianza para cada puntuación de habilidad se pueden observar en el gráfico adjunto. Se puede notar que entre -2 y -.05, el intervalo de confianza mantiene el radio más bajo de alrededor de 1 unidad logit.
7.3.5 Ajuste del modelo
Para evaluar el modelo, se puede reucrrir al SRMSR (standardized root mean square root of squared residuals, Maydeu-Olivaras, 2013), el cual se desea menor a 0.08. En el caso del ejemplo de Estadística el valor fue
SRMSR
0.02983104 Por otro lado, se puede comparar el ajuste del modelo con el ajuste de otros modelos para determinar cuál se ajusta mejor a los datos. Un modelo ajsuta mejor que otro si presenta un AIC y un BIC menor que el otro modelo o si esu verosimilitud es significativamente mayor. En la siguiente tabla se compara el ajuste dado por el modelo de Rasch y el modelo de 2 parámetros
Likelihood Ratio Table
AIC BIC log.Lik LRT df p.value
fitRasch 3902.67 3933.32 -1944.34
fit2pl 3874.98 3936.28 -1923.49 41.69 7 <0.0017.3.6 Sintaxis en R
Cargar la base de datos
BASE<-read.csv("BASE_Est9.csv",sep=",")Seleccionar el conjunto de ítems
ITEMSc<-BASE[,28:34]Estimar los modelos de Rasch, 1 y 2 parámetros
library(ltm)
fitRasch <- rasch(ITEMSc, constraint = cbind(ncol(ITEMSc) + 1, 1))
fit1pl <- rasch(ITEMSc)
fit2pl <- ltm(ITEMSc~z1)Ver los coeficientes de los ítems del modelo de 2 parámetros
Res<-coef(fit2pl)
ResEstimar las habilidades de las personas en el modelo de 2 parámetros
pp<-factor.scores(fit2pl, ITEMSc)
theta<-(pp$score.dat)$z1
se<-(pp$score.dat)$se.z1Habilidad y error estándar para la persona 1 en el modelo de 2 parámetros
theta[1]
se[1]Graficar una curva característica del ítem en el modelo de 2 parámetros
plot(fit2pl, items =1)Gráficar varias curvas características del ítem en el modelo de 2 parámetros
plot(fit2pl, items =c(1,2) )Graficar la función de información en el modelo de 2 parámetros
plot(fit2pl, type = "IIC", items = 0, lwd = 2)Evaluar el ajuste global del modelo de dos parámetros
library(TAM)
fit0 <- tam.mml.2pl( ITEMSc )
Res0 <-tam.modelfit(fit0)
Res0$fitstat[3]Comparar el ajuste de dos modelos
anova(fitRasch,fit2pl)7.3.7 Guía de trabajo 1
Utilice los ítems 13 a 17 de la base de conocimientos de Estadística y Probabilidad de la base, para contestar las siguientes preguntas.
Estime los coeficientes de los ítems del modelo de 2 parámetros de Teoría de Respuesta al Ítem (1 punto).
Para el ítem más difícil de la base de datos realice los siguientes análisis:
- Presente su curva característica del ítem (1 punto).
- Determine las probabilidades de acierto de una persona con una habilidad de 0 logits y otra con una habilidad de 1 logit (2 puntos).
- Determine el nivel de dificultad y discriminación obtenido según los cirterios establecidos (2 puntos).
Calcule el intervalo de confianza de la habilidad para la primera persona de la base de datos. Presente todos los cálculos realizados (2 puntos).
Determine si el modelo de TRI de dos parámetros presenta un mejor ajuste que el modelo de Rasch y el modelo de 1 parámetro (3 puntos).
7.4 Modelo de 3 parámetros
Este modelo descompone la probabilidad de acierto de un ítem en dos partes: una asociada al azar y otra asociada al efecto de la habilidad de las personas y las propiedades del ítem. El parámetro del azar está representado por \(c_i\) y representa una cota inferior de la probabilidad de acierto en el reactivo. La fórmula de este modelo viene dada por:
\[P(X_{ij}=1|\theta_j,a_i,b_i,c_i)=c_i+(1-c_i)\frac{e^{a_i(\theta_j-b_i)}}{1+e^{a_i(\theta_j-b_i)}}\]
En un ítem con un valor de \(c_i=.10\), junto con los paráemtros \(a_i=1.5\) y \(b_i=1\), se tendría la siguiente curva característica del ítem:
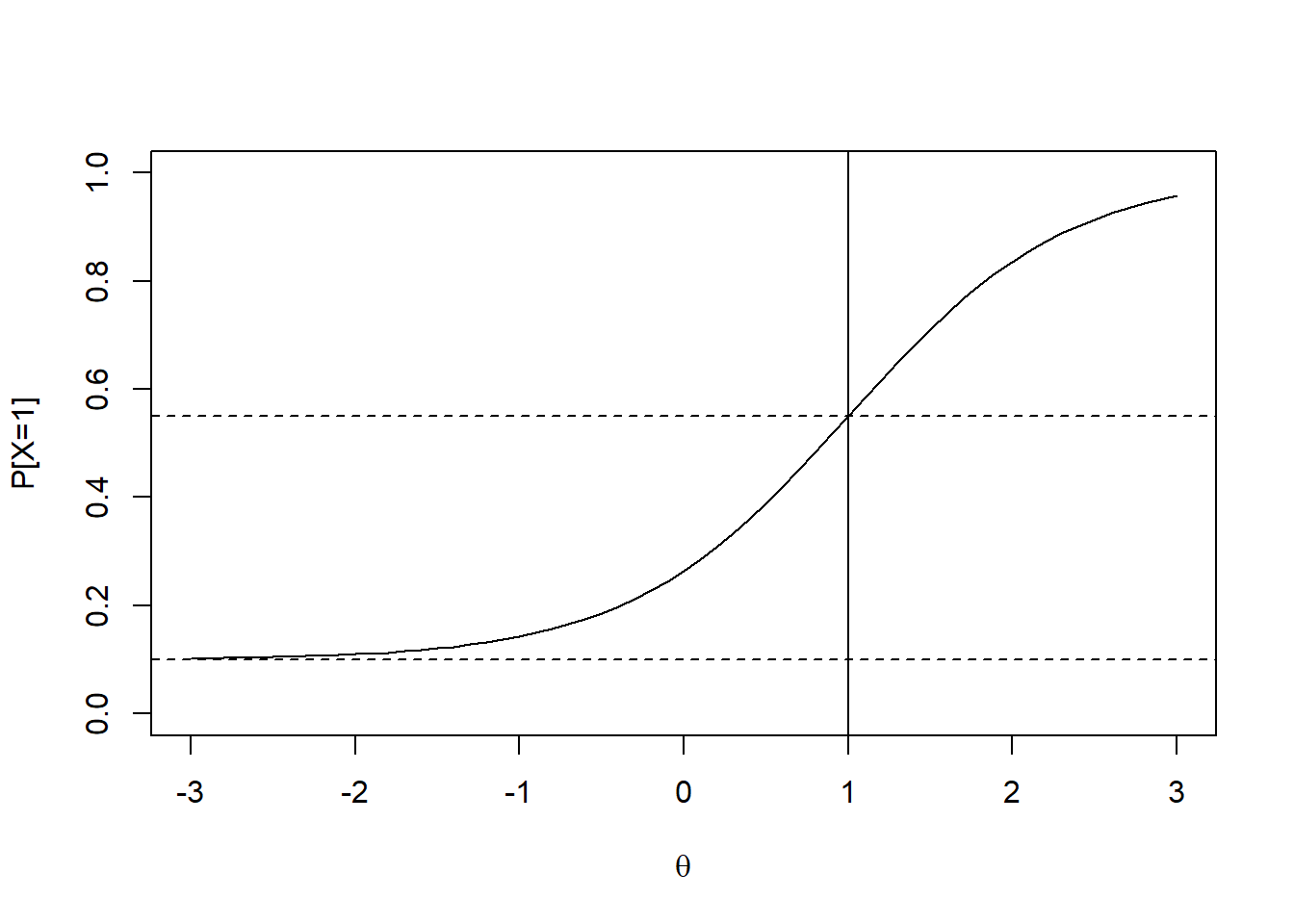
Es importante mencionar que las interpretaciones matemáticas de los parámetros de dificultad y discriminación deben ser adaptadas en función de la fórmula. En este caso, la dificultad será el valor de habilidad donde se alcanza una probabilidad de \(0.5+0.5c_i\); mientras que la recta de la pendiente tangente en \(b_i\) pasa a \((1-c_i)a_i/4\).
7.4.1 Ejemplo
A continuacion se presentan los coeficientes del modelo de 3 parámetros estimado en la dimensión Estadística de la base de ítems de conocimientos de Estadística y Probabilidad. En el ítem en la posición 5 (D6) aparece un parámetro de adivinación con un valor considerablemente superior a 0, en este ítem se puede observar que los parámetros de dificultad y discriminación aumentan ligeramente en comparación con el modelo de 2 parámetros, no obstante, este cambio es engañoso dado que las fórmulas para \(a\) y \(b\) son distintas cuando el \(c\) es distinto de 0.
b_1p a_1p b_2p a_2p b_3p a_3p c_3p
D2 -2.32 1.42 -2.10 1.70 -2.09 1.72 0.00
D3 -0.03 1.42 -0.04 1.05 0.03 1.10 0.03
D4 -2.87 1.42 -2.41 1.95 -2.42 1.94 0.00
D5 -0.45 1.42 -0.49 1.24 -0.50 1.23 0.00
D6 -1.02 1.42 -0.92 1.76 -0.70 2.10 0.13
D7 -0.40 1.42 -0.43 1.30 -0.43 1.30 0.00
D8 -1.20 1.42 -1.09 1.72 -1.09 1.71 0.00En el gráfico adjunto se presenta la curva característica del ítem en la posición 5. Se puede observar que el ítem presenta una asíntota horizontal en \(y=.13\).
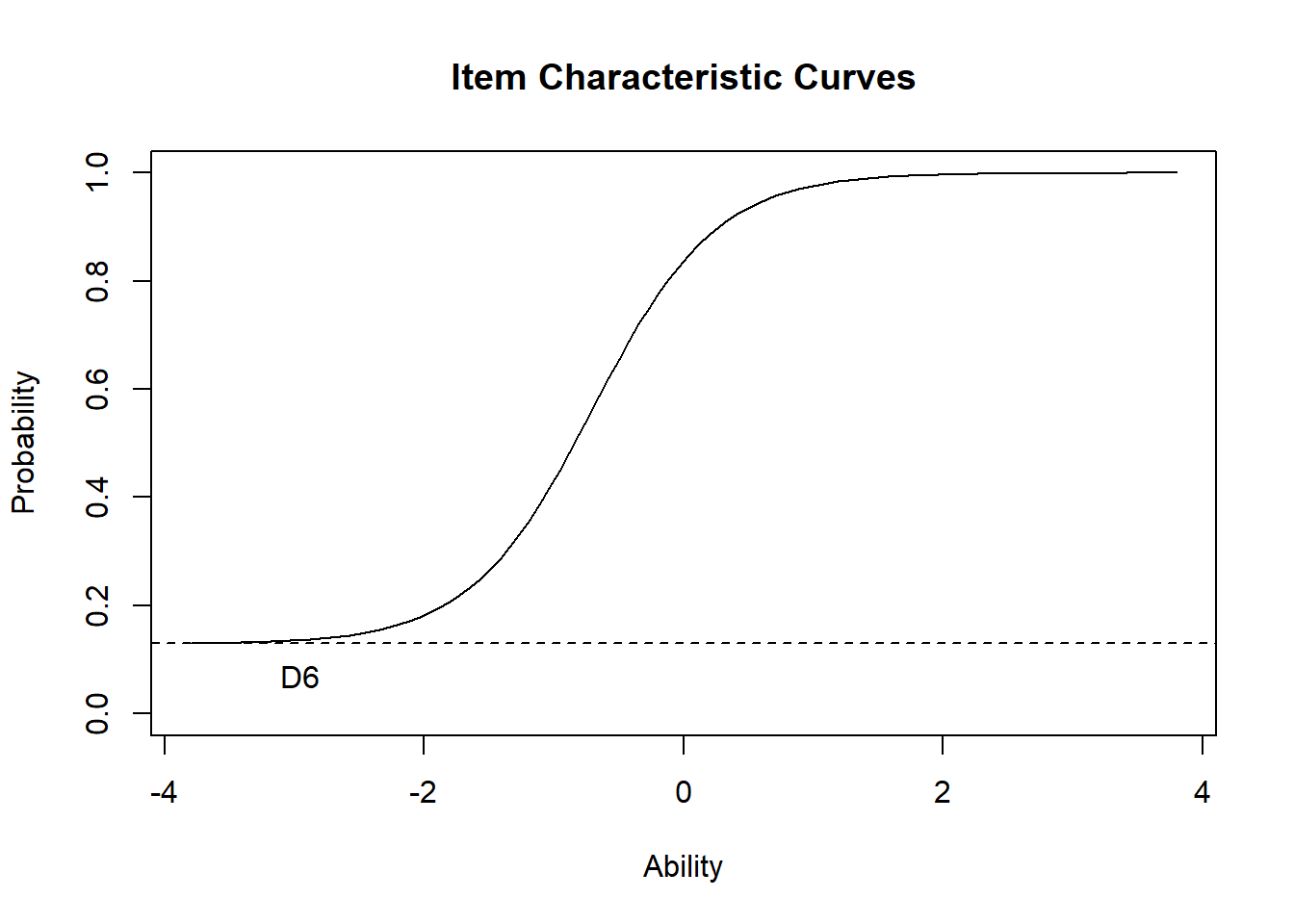
A continuación, se presenta la prueba de la razón de versoimilitudes entre el modelo de 2 parámetros y el modelo de 3 parámetros. Se puede observar que la adición del parámetro de adivinación no ayudó a mejorar la explicación de los datos, ya que no se encontró evidencia para rechazar la hipótesis nula de igualdad de ajustes entre modelos. Por tanto, el modelo que mejor explica los datos es el modelo de 2 parámetros.
Likelihood Ratio Table
AIC BIC log.Lik LRT df p.value
fit2pl 3874.98 3936.28 -1923.49
fit3pl 3888.42 3980.37 -1923.21 0.56 7 0.9997.4.2 Sintaxis en R
Cargar la base de datos
BASE<-read.csv("BASE_Est9.csv",sep=",")Seleccionar el conjunto de ítems
ITEMSc<-BASE[,c(28:34)]Estimar el modelo
library(ltm)
fit3pl <- tpm(ITEMSc,, max.guessing=.33)Ver los coeficientes de los ítems del modelo de 2 parámetros
Res<-coef(fit3pl)
ResEstimar las habilidades de las personas en el modelo de 3 parámetros
pp<-factor.scores(fit3pl, ITEMSc)
theta<-(pp$score.dat)$z1
se<-(pp$score.dat)$se.z1Habilidad y error estándar para la persona 1 en el modelo de 3 parámetros
theta[1]
se[1]Graficar una curva característica del ítem en el modelo de 3 parámetros
plot(fit3pl, items =5)Gráficar varias curvas características del ítem en el modelo de 3 parámetros
plot(fit3pl, items =c(1,5) )Graficar la función de información en el modelo de 3 parámetros
plot(fit3pl, type = "IIC", items = 0, lwd = 2)Evaluar el ajuste global del modelo de dos parámetros
library(TAM)
fit0 <- tam.mml.3pl( ITEMSc )
Res0 <-tam.modelfit(fit0)
Res0$fitstat[3]Comparar el ajuste de dos modelos
fit2pl<-ltm(ITEMSc~z1)
anova(fit2pl,fit3pl)7.4.3 Guía de trabajo 2
Utilice los ítems de la base de conocimientos de Estadística y Probabilidad, para contestar las siguientes preguntas.
Justifique por qué 2 factores son suficientes para explicar la variabilidad de los ítems de la base de datos.
Determine los ítems que cargan en cada uno de los dos factores (use un punto de corte de .28). Denomine al primer factor Prob y al segundo Est.
Calcule los alfa de Cronbach de Est y Prob.
Calcule las dificultades y discriminaciones ítem-total de los ítems de Prob.
Estudie el comportamiento de las opciones del segundo ítem de la dimensión Prob (considere que las columnas con las respuestas originales son las 18 al 22).
Determine las dificultades de los ítems de la dimensión Prob con el modelo de Rasch
Determine los infit y outfit de los items de la dimensión Prob
Determine las dificultades y discriminaciones de los ítems de la dimensión Prob con el modelo de TRI de dos parámetros
Calcule el modelo de 3 parámetros en la dimensión Prob.
- Determine si algún ítem presenta un parámetro de adivinación considerable.
- Determine si el modelo de 3 parámetros presenta una mejora significativa del modelo con respecto al modelo de 2 parámetros.
7.5 Referencias
Baker, F. B. (2001). The basics of item response theory. Eric.
https://scholarworks.umass.edu/cgi/viewcontent.cgi?article=1470&context=pare