8 Modelos politómicos de Teoría de Respuesta al Ítem

Los modelos politómicos de Teoría de Respuesta al Ítem modelan la probabilidad de respuesta de cada categoría o alternativa presente en un ítem, en función de la habilidad evaluada en los individuos y un conjunto de parámetros del ítem. La función de probabilidad de selección de cada categoría se denomina Curva Característica de la Categoría (CCC).

Los modelos más sencillos son el Modelo de Escala de Calificación (MEC) y el Modelo de Crédito Parcial (MCP), los cuales se basan en los supuestos del Modelo de Rasch y permiten analizar puntuaciones de escalas. En ambos modelos, se estiman parámetros para las parejas de categorías adyacentes, los cuales se denominan umbrales. Un umbral \(b_k\) indica el nivel en el constructo en el que la categoría \(k+1\) se vuelve más probable que la categoría \(k\).

La diferencia entre el MEC y el MCP es que en el primero se supone que los umbrales están a la misma distancia en todos los ítems, por lo cual en cada ítem los umbrales son una traslación de los obtenidos en otros ítems; en cambio, en el MCP los umbrales varían las distancias internas, entre los ítems. Lo anterior implica que el MEC requiere estimar menos parámetros que el MCP.

Otros modelos politómicos son el Modelo de Respuesta Graduada y el Modelo Nominal, los cuales representan las probabilidades de las categorías de respuesta con el uso de más parámetros. El MRG agrega 1 parámetro más por ítem con respecto al MCP, mientras que el MN agrega \(k-1\) parámetros por ítem con respecto al MCP.

8.1 Modelo de Escala de Calificación (Rating Scale Model)

Este modelo constituye una extensión del modelo dicotómico de Rasch a ítems politómicos ordinales con el mismo tipo de categorías. El modelo se basa en el supuesto de que la probabilidad de selección de las categorías adyacentes describe una curva logística.

Las curvas características de las categorías del MEC describen la probabilidad de seleccionar una categoría en función de la habilidad de los individuos y los umbrales de las categorías de respuestas adyacentes. Estos umbrales indican el punto en que la categoría \(k+1\) se vuelve más probable que la categoría \(k\). Además, los umbrales se encuentran a la misma distancia en todos los ítems.

Los umbrales se obtienen a partir de los umbrales base \(b_k\) para las \(K-1\) parejas de categorías adyacentes y los parámetros de localización de los ítems (\(c_i\)). El valor \(c_i\) indica cuántas unidades deben sustraerse de los umbrales base para generar los umbrales de los ítems. De esta manera, los umbrales de las categorías, en el ítem \(i\), corresponden a \(b_k-c_i\)

Las funciones de respuesta de categoría de un ítem con \(K\) categorías están dadas por

\[P_{ik}(\theta)=\frac{exp{\sum_{k'=1}^{k-1} (\theta-b_{k'}+c_i)}}{\sum_{r=1}^{K} \exp{\sum_{k'=1}^{r-1} (\theta-b_{k'}+c_i)}}\] De esta manera, en un ítem con 3 categorías se tendrían las siguientes ecuaciones:

\[P_{i1}(\theta)=\frac{1}{ 1+exp{(\theta-b_{1}+c_i)} + exp{(\theta-b_{1}+\theta-b_{2}+2c_i)} }\]

\[P_{i2}(\theta)=\frac{exp{(\theta-b_{1}+c_i)}}{ 1+exp{(\theta-b_{1}+c_i)} + exp{(\theta-b_{1}+\theta-b_{2}+2c_i)} }\]

\[P_{i3}(\theta)=\frac{exp{(\theta-b_{1}+\theta-b_{2}+2c_i)}}{1+exp{(\theta-b_{1}+c_i)} + exp{(\theta-b_{1}+\theta-b_{2}+2c_i)} }\]

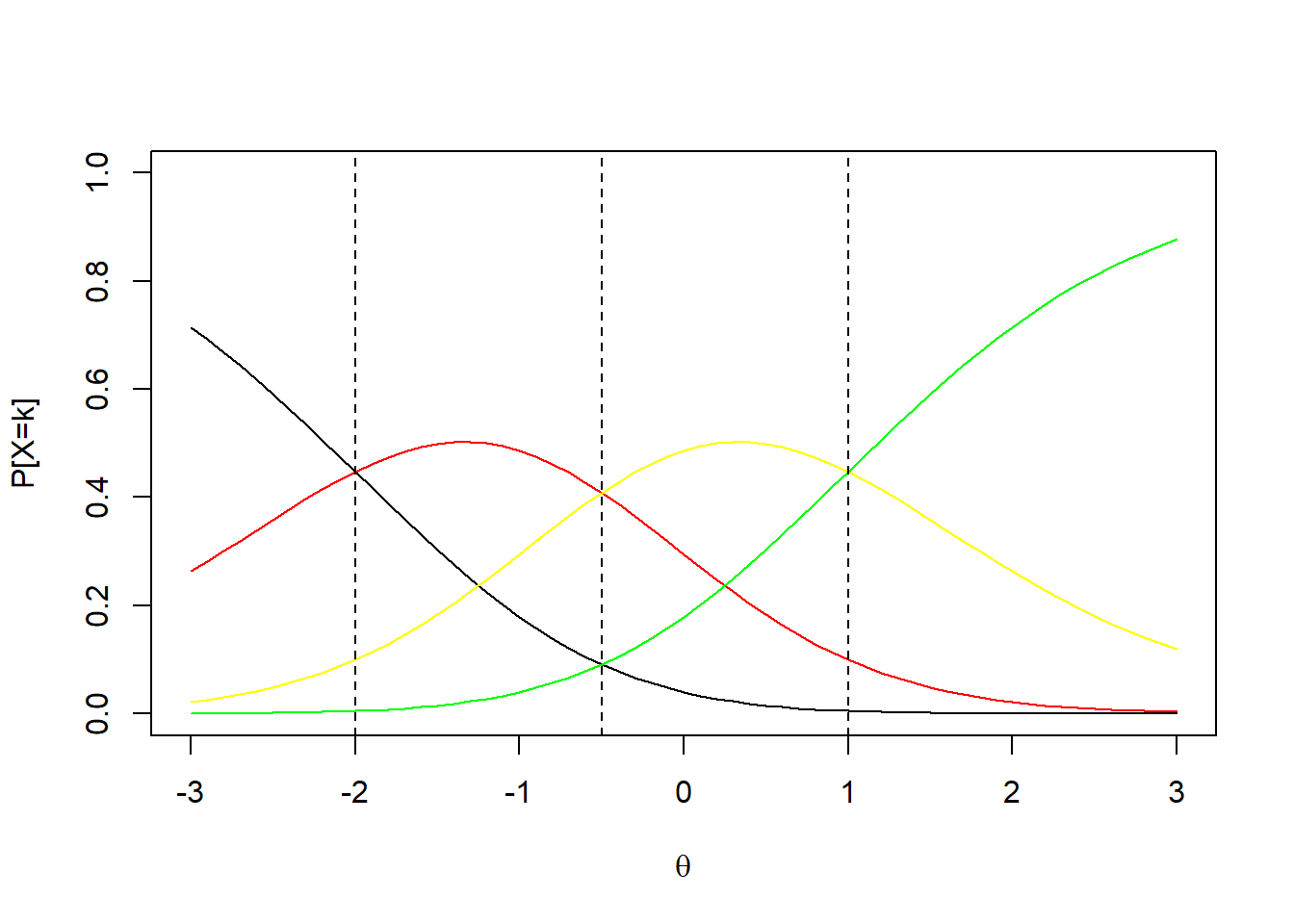
En un ítem de 4 categorías en el que \(b_{i1}=-1.5\), \(b_{i2}=0\) y \(b_{i3}=1.5\) se tendrían las siguientes curvas características de las categorías de respuesta:

8.1.1 Aplicación del modelo

A continuación se presentan los resultados de estimar el modelo de escala de calificación en los ítems de la base de Precoupación.

       b1    b2     c
PR1 -4.27 -1.96  0.00
PR2 -4.27 -1.96 -2.85
PR3 -4.27 -1.96 -1.86
PR4 -4.27 -1.96 -2.19
PR5 -4.27 -1.96 -0.26
PR6 -4.27 -1.96 -1.10
PR7 -4.27 -1.96 -1.64
PR8 -4.27 -1.96 -2.51
PR9 -4.27 -1.96 -2.31

Se puede observar que en el ítem en la posición, se alcanza el primer umbral en -1.42 (-4.27- -2.85) y que el segundo umbral se alcanza en 0.89 (-1.96- -2.85). Con base en lo anterior, la categoría 2 se vuelve más probable que la 1 en -1.42 y la categoría 3 se vuelve más probable que la 2 en 0.89.

8.1.2 Estimación de la habilidad de los individuos

Como en todos los modelos de medición, el objetivo es determinar el nivel de los individuos en el constructo. A continuación se presentan las habilidades y errores estándar de los primeros 5 individuos de la base de datos.


Method:  EAP

Empirical Reliability:

    F1 
0.8636

  P1 P2 P3 P4 P5 P6 P7 P8 P9 Punt   Hab   ee
1  0  0  0  0  0  0  0  0  0    0 -4.78 0.70
2  0  0  0  1  1  0  1  0  0    3 -3.32 0.64
3  0  0  0  1  1  2  2  0  1    7 -1.95 0.55
4  0  0  0  1  2  0  0  0  0    3 -3.32 0.64
5  0  1  1  1  1  1  1  0  1    7 -1.95 0.55

Note que los individuos 2 y 4 poseen la misma habilidad estimada, a pesar de tener patrones de respuestas distintas. Lo anterior se debe a que al igual que en Rasch dicotómico, las personas con la misma puntuación presentan la misma habilidad estimada.

8.1.3 Extrapolación de los análisis del modelo de Rasch

   Punt        hab
1     0 -3.4472019
2     1 -2.4921962
3     2 -1.6076389
4     3 -1.0146109
5     4 -0.5438887
6     5 -0.1404547
7     6  0.2223082
8     7  0.5602856
9     8  0.8842743
10    9  1.2023564
11   10  1.5211473
12   11  1.8466714
13   12  2.1852739
14   13  2.5450479
15   14  2.9385717
16   15  3.3892047
17   16  3.9498863
18   17  4.7903162
19   18  5.6987530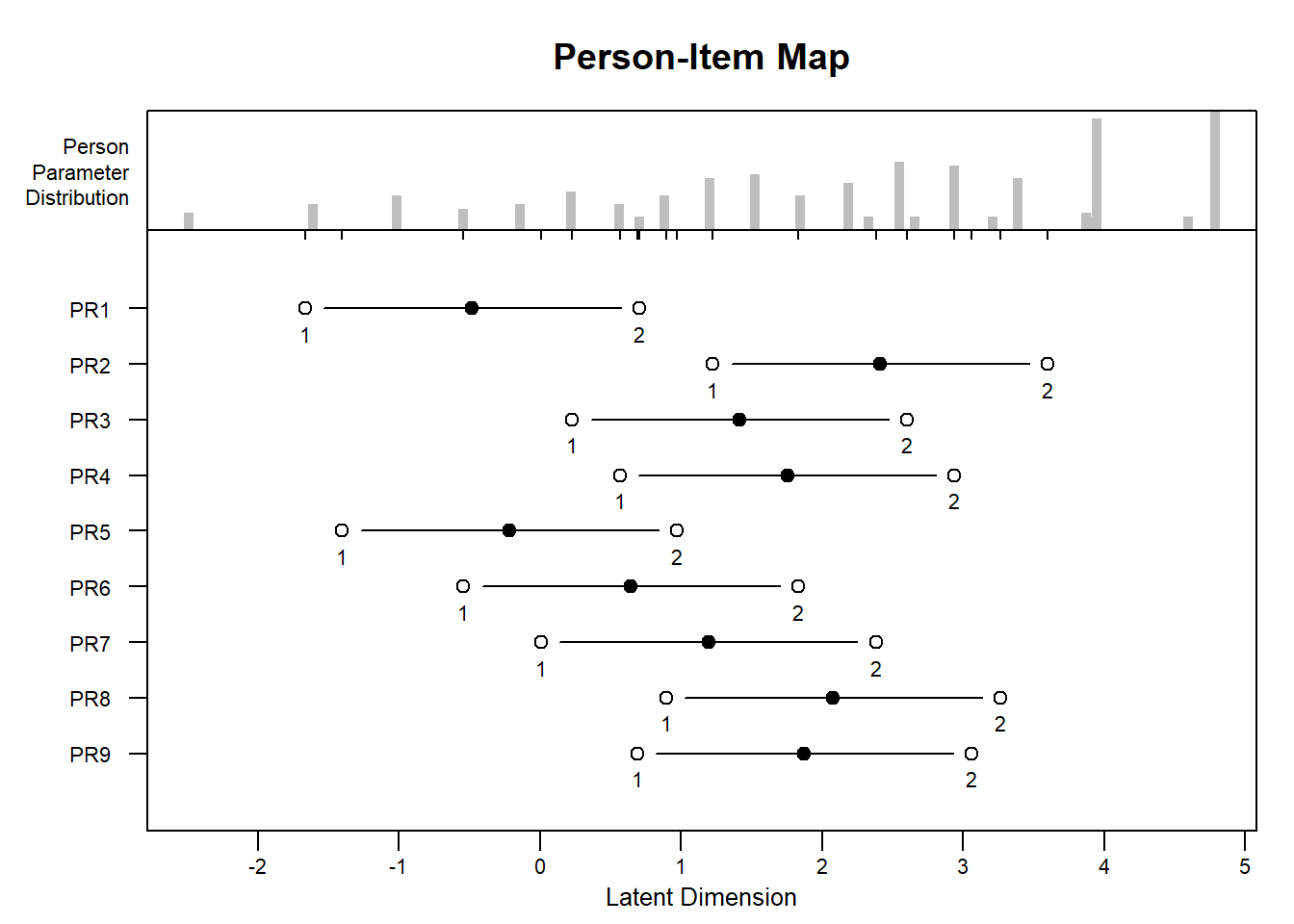

8.2 Modelo de Crédito Parcial

Este modelo también es una variante del modelo de Rasch para ítems politómicos ordinales y también se basa en la modelación de la probabilidad del cambio entre categorías adyacentes. La diferencia con el modelo previo es que este no supone que los umbrales mantienen las mismas separaciones en todos los ítems. En vista de lo anterior este modelo es útil para ítems con distintos tipos de escalas.

En vista del plantemiento previo no se requieren localizaciones de los ítems, sino de las categorías. Lo anterior lleva a que la fórmula de este modelo proponga umbrales para cada combinación de categorías adyacentes (\(k\)y \(k+1\)) en cada ítem (\(b_{ik}\)).

Las funciones de respuesta de categoría del ítem de las \(K\) categorías están dadas por

\[P_{ik}(\theta)=\frac{exp{\sum_{c=1}^{k-1} (\theta-b_{ic})}}{\sum_{r=1}^{K} \exp{\sum_{c=1}^{r-1} (\theta-b_{ic})}}\] De esta manera, en un ítem con 3 categorías se tendrían las siguientes ecuaciones:

\[P_{i1}(\theta)=\frac{1}{ 1+exp{(\theta-b_{i1})} + exp{(\theta-b_{i1}+\theta-b_{i2})} }\]

\[P_{i2}(\theta)=\frac{exp{(\theta-b_{i1})}}{ 1+exp{(\theta-b_{i1})} + exp{(\theta-b_{i1}+\theta-b_{i2})} }\]

\[P_{i3}(\theta)=\frac{exp{(\theta-b_{i1}+\theta-b_{i2})}}{1+exp{(\theta-b_{i1})} + exp{(\theta-b_{i1}+\theta-b_{i2})} }\]

En un ítem de 4 categorías en el que \(b_{i1}=-.82\), \(b_{i2}=.53\) y \(b_{i3}=1.5\) se tendrían las siguientes curvas características de las categorías de respuesta:

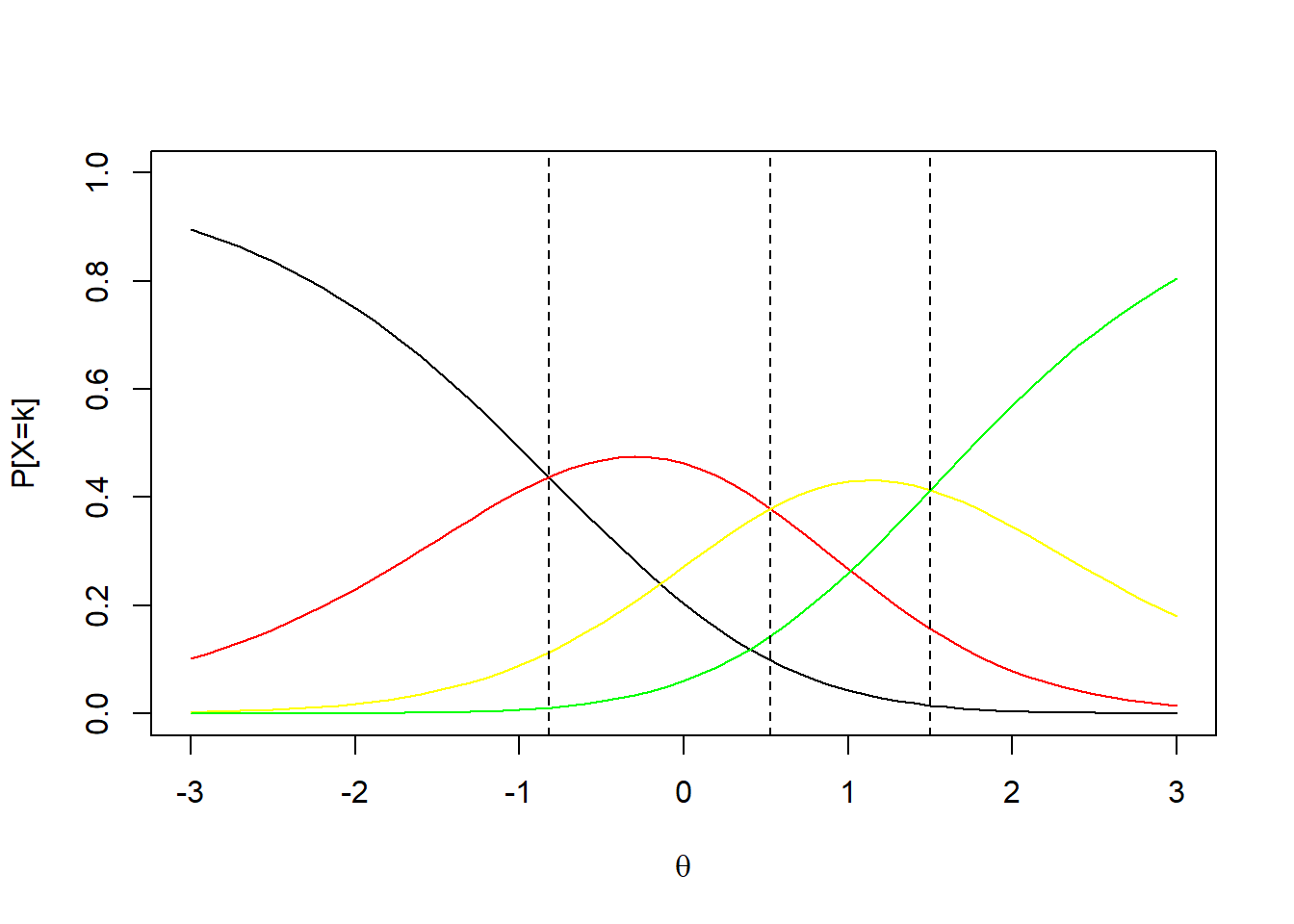
Note que \(b_{i1}\) indica el punto de habilidad en el que la categoría 2 se vuelve más probable que la 1. En general el coeficiente \(b_{ij}\) indica el punto en que la categoría \(j+1\) se vuelve más probable que la \(j\).

8.2.1 Ejemplo de una aplicación del modelo

Los coeficientes del modelo de crédito parcial estimado en los ítems de Preocupación son los siguientes:

    a    b1    b2
PR1 1 -4.83 -1.83
PR2 1 -1.61  1.03
PR3 1 -2.35 -0.16
PR4 1 -2.53  0.49
PR5 1 -3.85 -1.77
PR6 1 -2.76 -1.07
PR7 1 -2.07 -0.67
PR8 1 -2.07  0.76
PR9 1 -1.72  0.16

Note que al igual que en el modelo de escala de calificación, el umbral entre las categorías 2 y 3 presenta su valor más alto en el ítem en la posición 2. Esto indica que en este ítem se requiere un mayor nivel de preocupación que en el resto de ítems, para que la probabilidad de la categorái 3 sea más plasible que la 2.

Note que la opción 2 se vuelve más probable que la opción 1 en el valor \(b_{11}=-1.61\) y que la opción 3 se vuelve más probable que la opción 2 en \(b_{12}=1.03\).

8.3 Modelo de Respuesta Graduada

Este modelo constituye una extensión del modelo dicotómico de dos parámetros a ítems politómicos. El modelo se basa en el supuesto de que la probabilidad de selección de una categoría mayor o igual a la \(k\)-ésima categoría con respecto a las categorías previas describe una curva logística semejante a la del modelo de 2 parámetros.

Las funciones de respuesta de categoría del ítem de las \(K\) categorías están dadas por

\[P_{ik}(\theta)= P^{*}_{ik}(\theta) - P^{*}_{i,k+1}(\theta) \] Con \(P_{ik}^{*}(\theta)\) la probabilidad de seleccionar la categoría \(k\) o una superior (en el caso de la \(K\)-ésima categoría la función de respuesta es \(P_{iK}^{*}(\theta)\)). La fórmula de \(P_{ik}^{*}(\theta)\) es

\[P_{ik}^{*}(\theta)=\frac{1}{1+\exp(-a_i(\theta-b_{i,k-1}))}\]

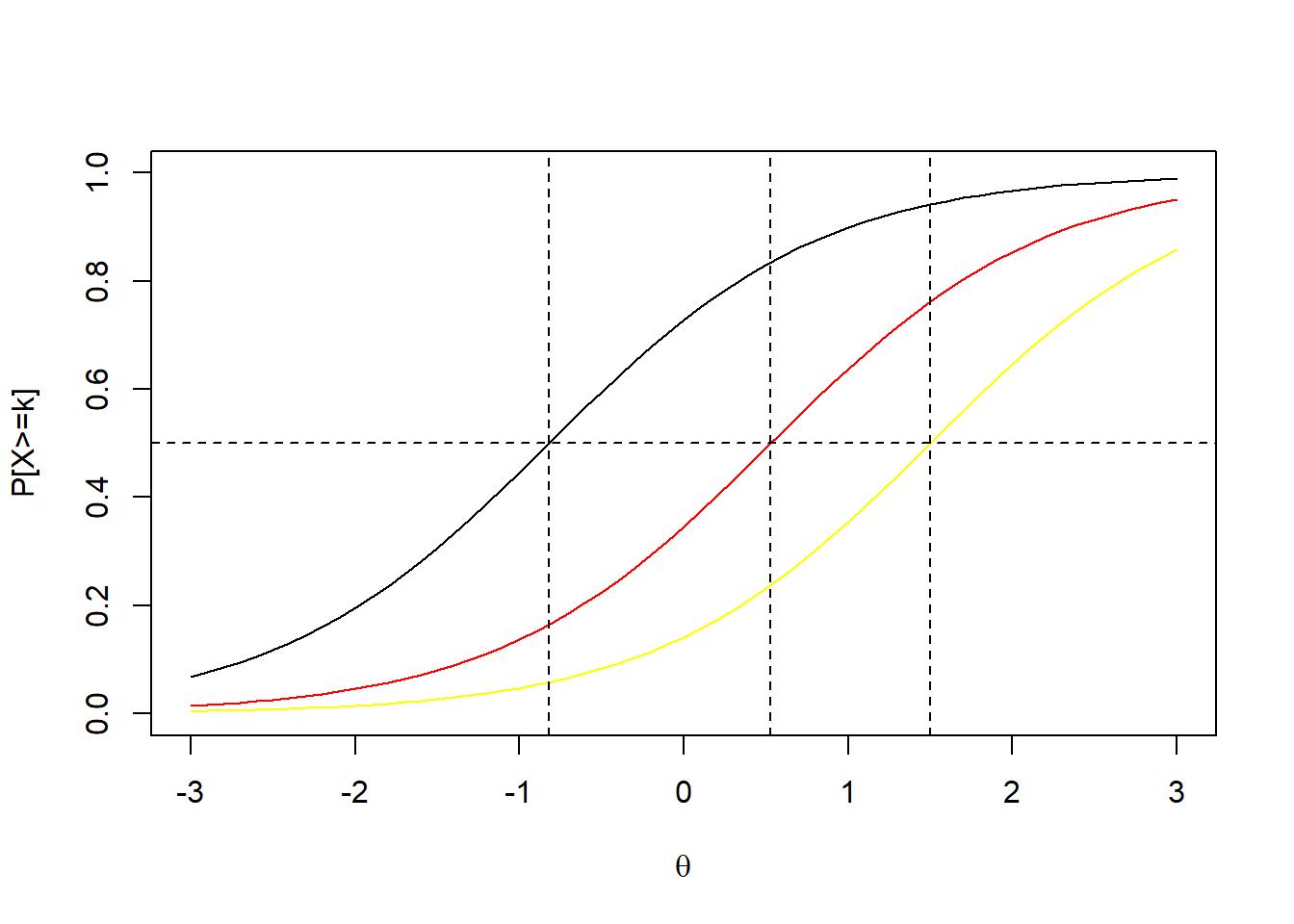
En un ítem de 4 categorías en el que \(b_{i1}=-.82\), \(b_{i2}=.53\), \(b_{i3}=1.5\) y \(a_i=1.2\) se tendrían las siguientes curvas características de las categorías de respuesta:

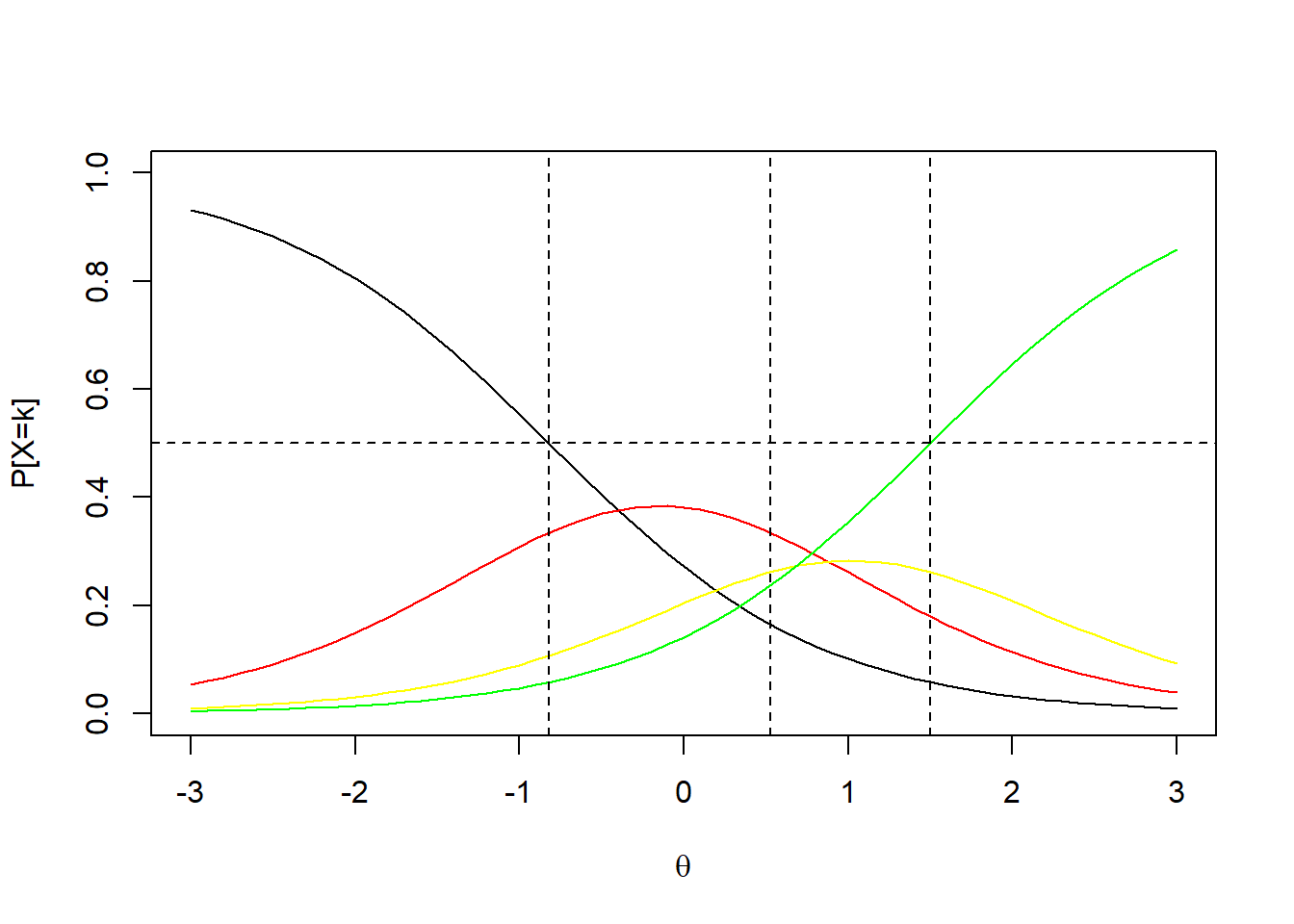
En este modelo los parámetros se vuelven más complejos de interpretar. Los \(b_{ik}\) indican los umbrales en que la categoría \(k+1\) o superior es más probable que las categorías \(k\) o inferiores. El \(b_{i1}\) y el \(b_{iK}\) son apreciables en la gráfica de las curvas características de las categorías, pero no comomo umbrales sino como puntos de localización. El valor de \(a_{i}\) indica la magnitud de la relación del constructo con el cambio de agregados.

En este modelo se vuelve relevante analizar la probabilidad de selección de cada categoría. Por ejemplo, en el gráfico previo la categoría amarilla alcanza menores probabilidades que la roja.

Note que antes de \(b_{i1}\) la categoría 1 tiene una alta probabilidad de ser seleccionada (mayor a 0.5), mientras que después \(b_{i3}\), la categoría 4 se vuelve muy probable.

Por otro lado, las curvas características operativas son las curvas que describen las modelaciones logísticas del paso de un agregado de categorías al agregado de categorías superior. Las curvas características operativas del ejemplo previo se presentan a continuación. En este gráfico si se logran visualizar las representaciones de los \(b_{ik}\)

8.3.1 Estimación del modelo

Los coeficientes del modelo de respuesta graduada estimado en la base de Preocupación son los siguientes:

           a         b1           b2
PR1 1.790547 -2.7996453 -0.941361425
PR2 1.991957 -0.8964373  0.605197432
PR3 3.241669 -1.1590711 -0.001079817
PR4 1.543481 -1.5446563  0.333144617
PR5 2.181048 -2.1147714 -0.811009501
PR6 2.858372 -1.4546345 -0.402513422
PR7 2.868218 -1.1389768 -0.202624325
PR8 2.329494 -1.0870197  0.422079078
PR9 2.884400 -0.9119254  0.163037162

Note que en el ítem 2, el valor de \(a\) es 1.99 lo cual se asocia a discriminaciones altas en las agrupaciones de categorías y, por ende, relaciones relevantes con el constructo. La categoría 1 deja de ser más probable que el resto en -0.89; mientras que la categoría 3 se vuelve más probable que el resto en 0.61. Por tanto, la categoría 3 es plausible para valores altos de preocupación, pero no para medios. En la mayoría del resto de ítems la categoría 3 se vuelve más probable que el resto desde valores medios.

8.4 Modelo Nominal

Este modelo estima la probabilidad de cada categoría de respuesta, sin considerar un orden particular en las opciones. No obstante, este modelo también puede ser utilizado para estudiar si el comportamiento de las categorías presenta el orden esperado. También es muy útil para analziar el comportamiento de opciones en los ítems de respuesta múltiple.

Las funciones de respuesta de categoría del ítem de las \(K\) categorías están dadas por

\[P_{ik}(\theta)= \frac{\exp{(a\cdot a_{ik}\theta+ d_{ik})}}{\sum_{k'=1}^K \exp{(a\cdot a_{ik'}\theta+d_{ik'})}} = \frac{\exp{(a\cdot a_{ik}[\theta-b_{ik}])}}{\sum_{k'=1}^K \exp{(a\cdot a_{ik'}[\theta- b_{ik'}])}}; b_{ik}= -a\cdot a_{ik}/d_{ik} \]

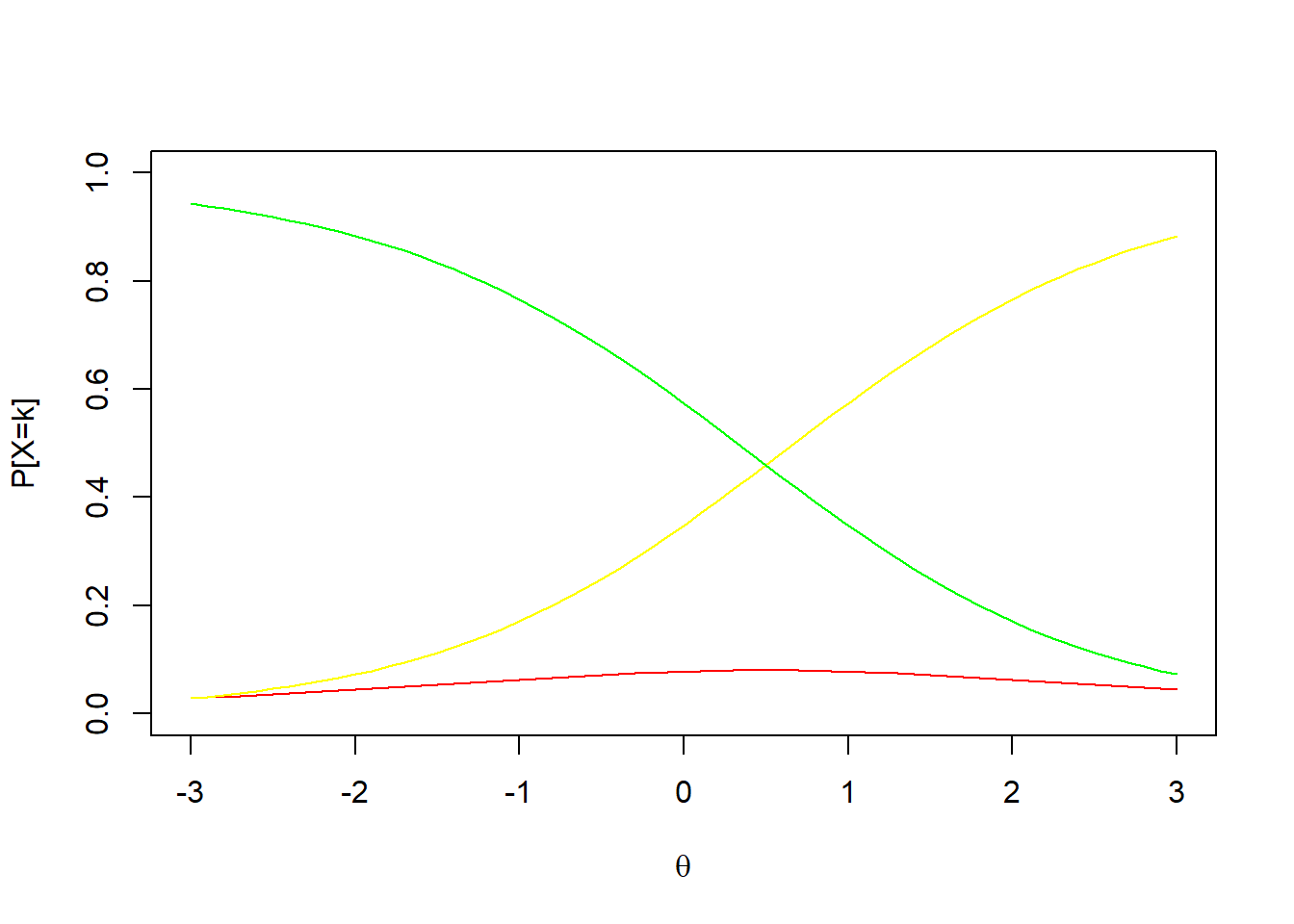
En un ítem de 3 categorías en el que \(d_{i1}=-1\), \(d_{i2}=0.5\), \(d_{i3}=1\) y \(a_{i1}=1\), \(a_{i2}=1.5\) y \(a_{i3}=0.5\) se tendrían las siguientes curvas características de las categorías de respuesta:

8.4.1 Ejemplo 1 de Estimación del modelo

El modelo nomila estimado en la base de los ítems de Preocupación presentó los siguientes resultados

      a1 ak0  ak1 ak2 d0   d1   d2
PR1 1.34   0 0.65   2  0 3.12 4.87
PR2 1.72   0 1.27   2  0 1.62 0.89
PR3 2.96   0 0.79   2  0 2.73 2.78
PR4 1.33   0 1.11   2  0 1.98 1.70
PR5 1.65   0 0.72   2  0 2.77 4.60
PR6 2.43   0 0.85   2  0 2.91 4.13
PR7 2.35   0 0.69   2  0 1.82 2.58
PR8 2.10   0 1.00   2  0 2.12 1.33
PR9 2.54   0 0.79   2  0 1.77 1.42

8.4.2 Contraste de ajustes

8.4.3 Ejemplo 2 de Estimación del modelo

Los coeficientes del modelo nominal estimado en los ítems de Estadística de la base de conocimientos de Estadística y Probabilidad son los siguientes:

     a1 ak0  ak1  ak2 ak3 d0    d1    d2    d3
P2 0.92   0 1.03 1.34   3  0  1.52  1.99  6.27
P3 1.24   0 2.48 1.80   3  0  4.31  3.31  4.78
P4 2.77   0 2.75 2.70   3  0 12.93 12.52 17.49
P5 1.34   0 1.81 2.41   3  0  3.67  4.59  5.62
P6 0.79   0 1.71 1.14   3  0  0.55  0.88  3.22
P7 0.57   0 1.28 0.89   3  0  0.00  0.25  1.78
P8 0.95   0 1.73 1.32   3  0  3.05  1.58  5.03

8.5 Sintaxis en R

Cargar la base

BASE<-read.csv("GTAI19.csv",sep=",")
ITEMS<-BASE[,c(2,5,8,9,13,16,20,22,26)]

Cargar el paquete para modelos politómicos de TRI

download.packages("mirt")
library(mirt)

Estimación de los modelos

library(mirt)
#Modelo de escala de respuesta
fit0 <- mirt(ITEMS, 1, 'rsm')
#Modelo de crédito parcial
fit1 <- mirt(ITEMS, 1, 'Rasch')
#Modelo de respuesta graduada
fit2 <- mirt(ITEMS, 1, 'graded')
#Modelo nominal
fit3 <- mirt(ITEMS, 1, 'nominal')
#Nota:En ítems de selección de respuesta se recomienda recodificar la clave a n, con
#n el número de opciones

Coeficientes de los ítems

coef(fit0, IRTpars=TRUE, simplify=TRUE)$items
#Nota: En el modelo de escala de respuesta el valor de c hay que cambiarle el signo
#Nota: En el modelo nominal, los valores de la fórmula se obtienen con IRTpars=FALSE

Habilidades de los individuos

hab<-fscores(fit0,full.scores = FALSE)
#datos de los primeros 5 individuos de la base
hab[1:5,]

Gráfico de las curvas características de las categorías

#La segunda entrada indica la posición del ítem que se desea graficar
itemplot(fit0, 1, xlim=c(-6,6))

Contraste del ajuste de los modelos

anova(fit0, fit3)

Análisis adicionales de los modelos politómicos de Rasch usando eRm

library(eRm)
#Modelo de escala de respuesta
fit0b<-RSM(ITEMS)
#Modelo de crédito parcial
fit1b<-PCM(ITEMS)
#Mapa de ítems-personas
plotPImap(fit0b)
#Tabla de puntuaciones vrs habilidades
pp<-person.parameter(fit0b)
pp
#Índices de ajuste de los ítems
itemfit(pp)
#Índices de ajuste de las personas
pf<-personfit(pp)
pf$p.outfitMSQ[pf$p.outfitMSQ>2]

8.6 Guía de trabajo

Utilice los ítems de la dimensión Emocionalidad de la base de la GTAI, para responder las siguientes preguntas.

Presente los coeficientes del Modelo de Escala de Respuesta e indique cuál es el ítem que presenta el umbral más alto entre las categorías 2 y 3 niveles. (2 pts)
Considere el ítem seleccionado en la pregunta 1.¿En cuáles niveles de habilidad se presentan los umbrales de las categorías adyacentes en el ítem seleccionado en la pregunta 1. Interprete estos valores. (2 pts)
Presente los coeficientes del Modelo de Crédito Parcial e indique el ítem con el umbral más alto entre las categorías 2 y 3. Interprete el valor de ese umbral.(2 pts)
Considere el ítem seleccionado en la pregunta 1. Presente el grafico de las curvas características de las categorías con cada uno de los cuatro modelos estudiados. ¿Cuál es el valor máximo de probabilidad, aproximado, que alcanza la categoría 2 en cada modelo? ¿En cuaáles modelos es una categoría plausible? (8 pts)
Determine cuál de los modelos se ajusta mejor a los datos. (2 pts)
Con base en el modelo seleccionado en la pregunta 5, estime los intervalos de confianza de habilidad de los primeros 5 individuos de la base. (2 pts)

8.7 Referencias

https://rpubs.com/Tarid/polyIRT_practice

https://uk.sagepub.com/sites/default/files/upm-assets/126580_book_item_126580.pdf