FC1 PR1 EM1 IN1 PR2
FC1 1.00 -0.16 -0.30 -0.37 -0.33
PR1 -0.16 1.00 0.47 0.33 0.63
EM1 -0.30 0.47 1.00 0.32 0.46
IN1 -0.37 0.33 0.32 1.00 0.59
PR2 -0.33 0.63 0.46 0.59 1.002 Análisis Factorial Exploratorio
2.1 Modelo
El Análisis Factorial Exploratorio (AFE) es una técnica estadística que busca explicar la variabilidad de un conjunto de variables observadas en un número menor de variables no observadas, denominas factores.
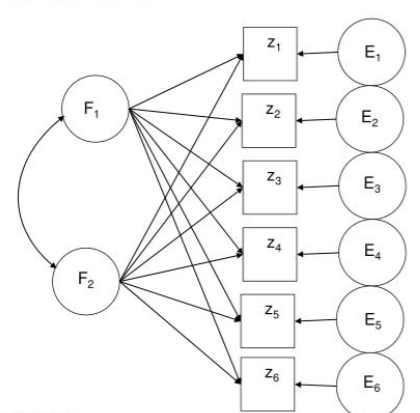
La importancia de esta técnica radica en que las variables no observadas pueden representar constructos relevantes de estudio y las variables observadas serían manifestaciones de estos constructos. Por tanto, el AFE permite explorar si existen constructos subyacentes a un conjunto de manifestaciones de interés.
La fórmula del AFE para \(n\) variables observadas explicadas por \(k\) factores es la siguiente:
\[ \begin{array}{l} x_1-\mu_1 = \lambda_{1,1}F_1+\lambda_{1,2}F_2+...+\lambda_{1,k}F_k+\varepsilon_1\\ x_2-\mu_2 = \lambda_{2,1}F_1+\lambda_{2,2}F_2+...+\lambda_{2,k}F_k+\varepsilon_2\\ \vdots\\ x_n-\mu_n = \lambda_{n,1}F_1+\lambda_{n,2}F_2+...+\lambda_{n,k}F_k+\varepsilon_n\\ \end{array} \]
Los coeficientes \(\lambda_{i,j}\) se denominan cargas factoriales. Además, la formulación de las ecuaciones previas implica que
\[\Sigma=Var(\mathbf{x})=\Lambda\Phi\Lambda^T+\Psi\].
En los casos con variables ordinales se busca aproximar la matriz de correlaciones policórica.
2.1.1 Supuestos teóricos
Los supuestos del modelo son los siguientes:
- \(\varepsilon_i\) y \(F_j\) son indepedientes.
- \(E(F)=0\)
2.1.2 Supuestos prácticos
- Estructura factorizable de la matriz de varianzas de las variables observadas.
- Linealidad de las variables.
El último supuesto no se cumple en datos dicotómicos o politómicos.
2.1.3 Ejemplo de las fórmulas del AFE aplicadas a un conjunto de datos
Para ejemplificar la aplicación de las fórmulas del AFE a un conjunto de datos se utilizarán los ítems de la GTAI, esta escala posee 29 ítems que son explicados por 4 factores.
En el caso de la GTAI se tienen las siguientes cargas factoriales de los ítems en los 4 factores mencionados:
\[ \begin{array}{l} x_1-\mu_1 = 0.12 F_1 +0.04 F_2+ 0.64 F_3 -0.16 F_4 +\varepsilon_1\\ x_2-\mu_2 = 0.82 F_1 -0.11 F_2+ 0.10 F_3 +0.01 F_4 +\varepsilon_2\\ \vdots\\ x_{29}-\mu_{29} = 0.02 F_1+0.85 F_2+0.08F_3+0.00F_4+\varepsilon_{29}\\ \end{array} \]
En el caso del ítem \(x_1\), con una estimación de los valores de los factores establecidos, se llega a la siguiente descomposición para los primeras 3 observaciones
\[ \begin{array}{llllll} 1-1.40 &= 0.12\cdot1.07 &+0.04\cdot0.83&+ 0.64\cdot0.58 &-0.16\cdot0.93 &-0.78\\ 2-1.40 &= 0.12\cdot0.50 &+0.04\cdot-0.46&+ 0.64\cdot1.26&-0.16\cdot-0.08 &-0.27\\ 1-1.40 &= 0.12\cdot-0.64 &+0.04\cdot-1.43&+ 0.64\cdot-0.22 &-0.16\cdot-0.17 &-0.16\\ \end{array} \]
Por otro lado, también se puede estimar la matriz de correlaciones por medio de la fórmula dada en el AFE. La matriz de correlacion observada de los primeros 5 ítems fue:
Mientras que la matriz de correlaciones estimada por el AFE de los primeors 5 ítems fue:
FC1 PR1 EM1 IN1 PR2
FC1 1.00 -0.15 -0.29 -0.32 -0.34
PR1 -0.15 1.00 0.40 0.30 0.54
EM1 -0.29 0.40 1.00 0.35 0.49
IN1 -0.32 0.30 0.35 1.00 0.48
PR2 -0.34 0.54 0.49 0.48 1.00Se puede notar que ambas matrices son my similares.
2.2 Fase preliminar del Análisis Factorial Exploratorio
2.2.1 Comprobación de supuestos
En primer lugar, se debe analizar si la matriz de correlaciones de los ítems presenta una estructura factorizable, es decir, distinta a la identidad. Para analizar esta característica existen dos métodos: el coeficiente KMO (>.70 es aceptable) y la prueba de esfericidad de Bartlett (H0: \(\Sigma=I\)).
En el caso de la GTAI se obtuvo que el índice fue mayor a .70, por lo cual tiene sentido aplicar un AFE. El valor del índice fue:
[1] 0.9000512Por su parte, la prueba de esferecidad de Bartlett fue significativa (\(p<.05\)), por lo cual se rechaza la hipótesis H0: \(\Sigma=I\), esto implica que la matriz posee correlaciones no nulas, que permiten realizar un AFE. El resultado de la prueba fue:
Bartlett test of homogeneity of variances
data: GTAI
Bartlett's K-squared = 138.38, df = 28, p-value < 2.2e-162.2.2 Determinación del número de factores del AFE
Existen muchos criterios para determinar el número de factores, los más utilizados son el scree plot y el análisis paralelo.
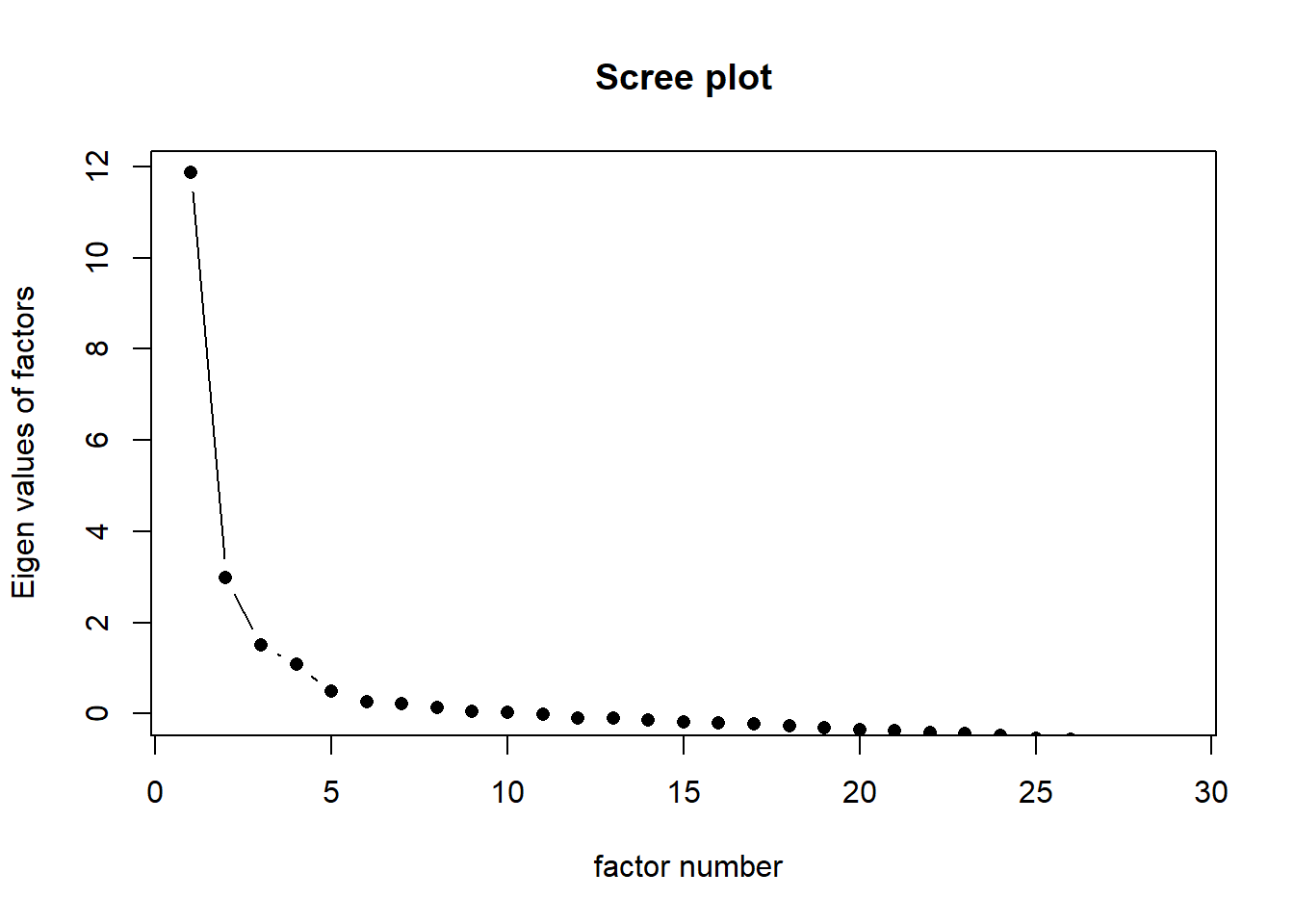
En el scree plot o gráfico de sedimentación se grafican los valores propios de la matriz de correlaciones de los ítems. En este criterio se retiene una cantidad de factores igual a los puntos previos al codo definitivo del gráfico (punto donde empieza una pseudo línea horizontal).
En la figura adjunta se observa el gráfico de sedimentación de la GTAI, en la cual se observa que el codo definitivo aparece en el punto 5, por lo cual se deben retener 4 factores.
En el análisis paralelo se compara el sree plot original con el de una matriz de datos aleatorios de mismo tamaño que la original. El número de factores se define como la cantidad de valores propios mayores a los obtenidos en la matriz de datos aleatorios. Este es el criterio más recomendado para definir el número de factores. En la figura adjunta también se observa que la cantidad de factores por retener en la GTAI debe ser 4.
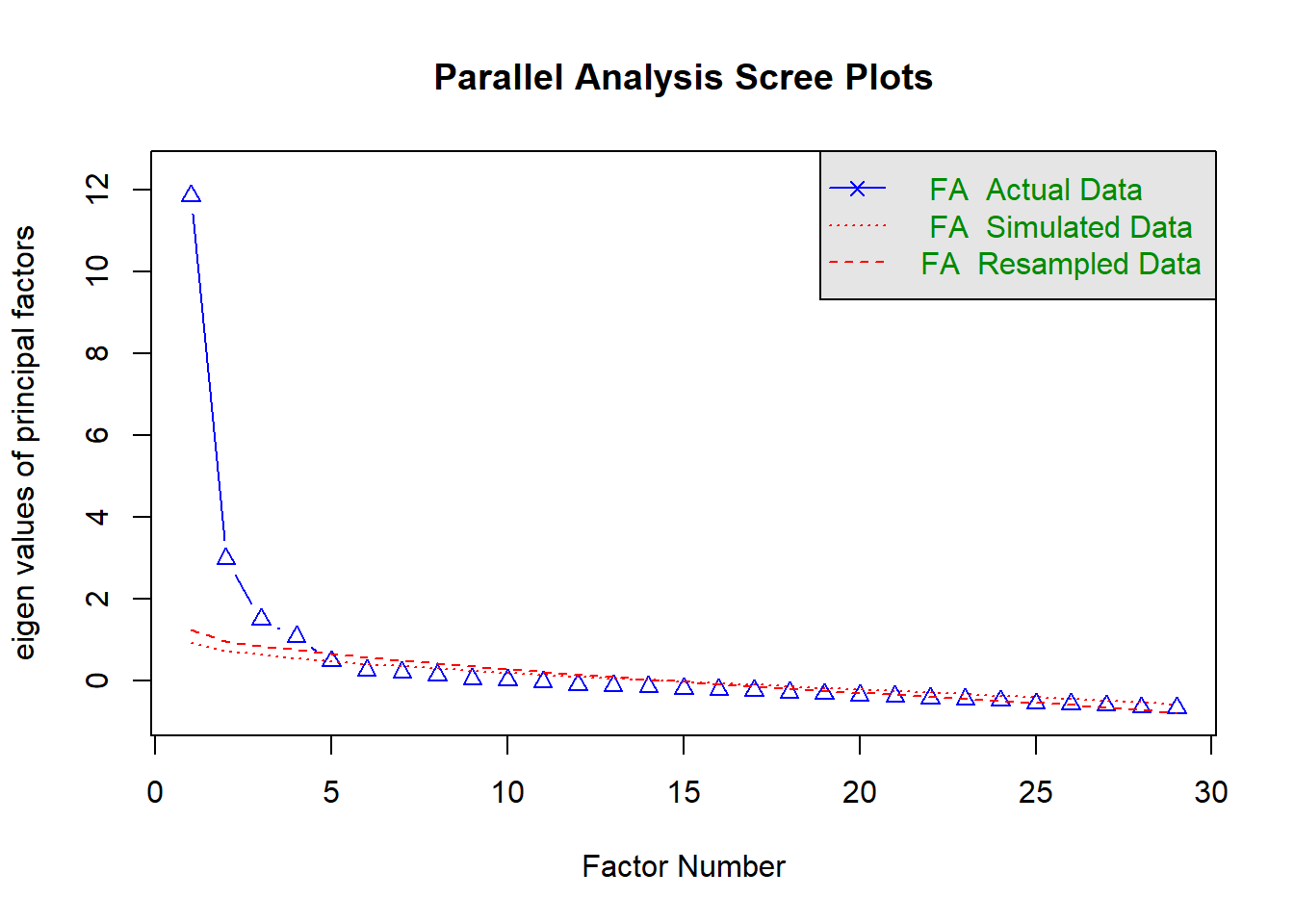
Parallel analysis suggests that the number of factors = 4 and the number of components = NA Otro elemento que se puede considerar en la determinación del número de factores es el porcentaje de varianza de los ítems explicada por cada uno de los factores. Se espera que cada factor explique al menos un 5% de la varianza compartida. Todos los valores obtenidos en la GTAI fueron mayores al 5%, sus valores fueron los siguientes:
WLS1 WLS2 WLS3 WLS4
Proportion Var 0.208766 0.1366518 0.1292343 0.09556021
Cumulative Var 0.208766 0.3454179 0.4746521 0.57021235Otro elemento a considerar en la determinación de factores es la diferencia entre los primeros dos autovalores, si el primero es 5 o más veces mayor que el primero se puede concluir que la escala posee un factor dominante y se puede proceder a trabajar con un solo factor.
2.3 Estimación e interpretación del AFE
El objetivo principal del AFE es identificar los factores que subyacen a los items. Para este objetivo se buscan los ítems con cargas factoriales relevantes en cada factor, por lo general con valores superiores a .30 en valor absoluto. Note que estos ítems son los que dependen con mayor fuerza del factor de interés, en otras palabras, son las manifestaciones más asociadas a las variables latentes de interés.
Existen mútliples métodos matemáticos que permiten determinar los valores buscados en el AFE, como máxima verosimilitud o residuos mínimos, los cuales son apropiados para variables continuas (el primero demanda el cumplimiento del supuesto de multinormalidad). El método recomendado para variables ordinales es mínimos cuadrados ponderados (wls) (Wood y Edwards, 2007).
Una vez determinado el número de factores y el método de estimación del Análisis Factorial Exploratorio se procede a calcular las cargas factoriales. En el caso de la GTAI, las cargas factoriales superiores a .30 fueron las siguientes:
WLS1 WLS2 WLS3 WLS4
FC1 -0.51 0.35
PR1 0.56 0.48
EM1 0.63
IN1 0.67
PR2 0.77
EM2 0.62
FC2 -0.67
PR3 0.74 0.31
PR4 0.64
IN2 0.48 -0.57
EM3 0.49 -0.33
FC3 -0.64 0.41
PR5 0.59 0.39
IN3 0.50 -0.53
EM4 0.59 0.43
PR6 0.72 0.39
EM7 0.53
IN4 0.58 -0.33
FC4 -0.61
PR7 0.75
EM5 0.68 0.36
PR8 0.74
IN5 0.51 -0.52
EM6 0.77
FC5 -0.59 0.41
PR9 0.73
EM8 0.75
FC6 -0.58 0.43
IN6 0.53 -0.51 0.35 En el caso de que hubiesen muchas variables que cargan en varios factores a la vez se puede recurrir a una rotación de la solución. Esta estrategia permite mejorar el algoritmo de identificación. Si se sospecha que los factores están correlacionados entre sí, se puede recurrir a una rotación oblimin o promax.
En el ejemplo de la GTAI se observa que casi todos los ítems cargan en dos factores, debido a esto se puede proceder a una rotación oblimin, cuyos valores son los siguientes:
WLS1 WLS2 WLS3 WLS4
FC1 0.44
PR1 0.71
EM1 0.54
IN1 0.45
PR2 0.55
EM2 0.41
FC2 0.76
PR3 0.77
PR4 0.47
IN2 0.81
EM3 0.32
FC3 0.84
PR5 0.76
IN3 0.73
EM4 0.77
PR6 0.79
EM7
IN4 0.54
FC4 0.51
PR7 0.73
EM5 0.70
PR8 0.63
IN5 0.75
EM6 0.44
FC5 0.61
PR9 0.69
EM8 0.35 0.47
FC6 0.74
IN6 0.93 Luego de que se obtienen una solución práctica, en la que la mayoría de ítems cargan en un solo factor, se puede proceder a identificar el constructo subyacente a cada factor.
En el caso de la GTAI los ítems con cargas factoriales altas en el factor 1 fueron: 2, 5, 8, 9, 12, 13, 16, 20, 22, 26 y 27, aunque este último carga de forma más alta en el factor 4. Todos estos ítems, excepto el 27, fueron construidos para la dimensión Preocupación de la escala GTAI, por lo cual tienen sentido concluir que el factor estudiado representa el constructo Preocupación. De igual manera, se concluye que los otros factores representan los constructos: interferencia, confianza y emocionalidad, respectivamente.
2.3.1 Otros resultados relevantes
En la estimación del AFE también se puede observar las comunalidades de los ítems, estas indican el porcentaje de varianza de los ítems explicada por los factores. Un ítem con una comunalidad baja no es explicado por los factores considerados, por tanto, no es una manifestación de ellos.
En el caso de la GTAI, las comunalidades de todos los ítems, excepto dos, fueron superiores a .40. Esos dos ítems deben ser analizados para ver si realmente son manifestaciones de los constructos evaluados. Los valores finales de las comunalidades fueron:
FC1 PR1 EM1 IN1 PR2 EM2 FC2 PR3
0.2774736 0.4158206 0.4533890 0.4389949 0.5295730 0.3672149 0.6607851 0.6477258
PR4 IN2 EM3 FC3 PR5 IN3 EM4 PR6
0.3713672 0.6408588 0.2472866 0.6723913 0.4762273 0.5449615 0.5636463 0.6119203
EM7 IN4 FC4 PR7 EM5 PR8 IN5 EM6
0.2043369 0.3917621 0.4079054 0.5979224 0.5290290 0.5614886 0.6192758 0.5331343
FC5 PR9 EM8 FC6 IN6
0.4281879 0.5815708 0.5608787 0.5318082 0.8070393 Otro elemento de interés en el AFE son las correlaciones entre los factores estimados, ya quees tos coeficeitnes brindadn una idea de las relaciones que se dan entre los factores identificados. En el caso de la GTAI las correlaciones observadas entre los factores Preocupación, Interferencia, Confianza y Emocionalidad (PR, IN, CN y EM) fueron moderadas, sus valores fueron:
WLS1 WLS2 WLS3 WLS4
WLS1 1.0000000 0.2715992 -0.3960800 0.4693013
WLS2 0.2715992 1.0000000 -0.4023958 0.2724457
WLS3 -0.3960800 -0.4023958 1.0000000 -0.3899358
WLS4 0.4693013 0.2724457 -0.3899358 1.00000002.4 Ajuste del modelo
Una vez estimado el modelo se debe analziar si este explicó apropiadamente los datos. Entre los índices de ajuste más comunes son el RMS (Root Mean Square Residual), el RMSEA (Root Mean Square Error of Approximation), el TLI (Tucker Lewis Index) y el BIC (Bayesian Information Criterion). El criterio de buen ajuste según el RMS es un valor menor a 0.08. Con el RMSEA se considera que hay un buen ajuste si este es menor a 0.08 y se concluye que es excelente, si este es menor a 0.05. Con el TLI se requiere un valor superior a 0.95 para un ajsute excelente; para un ajuste aceptable se puede relajar a 0.90. Por su parte, el BIC es un criterio para comparar modelos, se prefieren los modelos con valores más bajos del BIC.
En el caso de la estimación con el método WLS, varios índices no pueden ser estimados. Uno que puede ser calulado es el RMS. En el caso de la GTAI este índice fue menor a .08,por lo ucal indicó un buen ajuste del modelo a los datos, su valor fue:
[1] 0.036441022.5 Código R del Análisis Factorial Exploratorio
Cargar la base donde están los reactivos.
BASE<-read.csv("GTAI19.csv", sep=",") #### DEFINIR BASEGenerar una base de ítems
ITEMS<-BASE[,c(1:29)] #### DEFINIR CONJUNTO DE ÍTEMSEstudiar si la matriz es factorizable con el KMO
library(psych)
KMOr<- KMO(ITEMS)
KMOr$MSAEstudiar si la matriz es factorizable con el test de Bartlett
bartlett.test(ITEMS)Determinar el número de factores con el análisis paralelo
fa.parallel(ITEMS,fa="fa",cor="poly")Comprobar que los factores aporten a la explicación
R<-polychoric(ITEMS)
fit<- fa(R$rho, nfactors=4, fm="wls") ### DEFINIR FACTORES
fit$Vaccounted[2:3,]Estimar el AFE con los factores definidos y usando rotación Oblimin (default de R)
fit<- fa(R$rho, nfactors=4, fm="wls") ### DEFINIR FACTORES
fit$loadings[1:29, ] ### INDICAR NÚMERO DE ÍTEMS DESPUÉS DE :Cálculo de comunalidades y correlaciones entre factores
fit$communalities
fit$PhiÍndice RMS
fit$rms2.6 Guía de trabajo 1
Elabore una pequeña descripción del constructo evaluado por la EAE https://www.ansiedadyestres.es/sites/default/files/rev/2022/anyes2022a9.pdf y de las dimensiones originales https://www.kerwa.ucr.ac.cr/bitstream/handle/10669/83636/Tesis-firmado-firmado.pdf?sequence=1 (p.32-33). Describa brevemente la estructura del instrumento: número de ítems y formato de los ítems; junto con la población evaluada (número de sujetos y distribución por género). [4 puntos]
Justifique por qué tiene sentido realizar un AFE de los ítems de la escala (usando el KMO y el test de Barttlet). [2 puntos]
Determine el número de factores de la escala sugerido por el análisis paralelo. Justifique su respuesta. [1 punto]
Calcule la varianza aportada por cada factor. Determine si tiene sentido o no mantener la cantidad de factores sugerida por el análisis pararalelo. Justifique su respuesta. [2 puntos]
Estime el AFE de la escala y use el valor 0.35 como criterio de carga. Presente una tabla con las cargas factoriales de los ítems. Marque con negrita las cargas factoriales superiores a 0.35. Los ítems que definen un mismo factor deben estar en un solo bloque, ordenados de forma descendente según la carga en el factor que definen. Al final de la tabla coloque los ítems que no cargaron en ningún factor o que cargan en varios factores, ordenados según la forma en que aparecen en la escala. [3 puntos]
Justifique si es necesario realizar una rotación o no [1 punto]
Asigne un nombre a cada uno de los factores establecidos. Justifique la asignación del nombre. [1 punto]
Presente la estructura final de la escala: cuántas dimensiones tiene y cuáles son sus nombres; cuáles ítems están en cada dimensión y; cuáles ítems quedaron fuera y por qué. [2 puntos]
Presente las correlaciones entre los factores estimados e interprete tres de ellas. [2 puntos]
Indique si el AFE presentó un buen ajuste a los datos. [2 puntos]
2.7 Referencias
Pérez, E. y Medrano, L. A. (2010). Análisis factorial exploratorio Bases conceptuales y metodológicas. Revista Argentina de Ciencias del Comportamiento, 2(1) 58-66. https://dialnet.unirioja.es/servlet/articulo?codigo=3161108
Lloret-Segura, S., Ferreres-Traver, A., Hernández-Baeza, A. y Tomás-Marco, I. (2014). El Análisis Factorial Exploratorio de los Ítems: una guía práctica, revisada y actualizada. Anales de Psicología, 30(3) 1151-1169. http://dx.doi.org/10.6018/analesps.30.3.199361
https://www.scielo.cl/scielo.php?script=sci_arttext&pid=S0718-22282023000200113 https://journals.sagepub.com/doi/epub/10.1177/0013164420942899 https://search.r-project.org/CRAN/refmans/EFA.dimensions/html/ROOTFIT.html https://journals.sagepub.com/doi/full/10.1177/0095798418771807