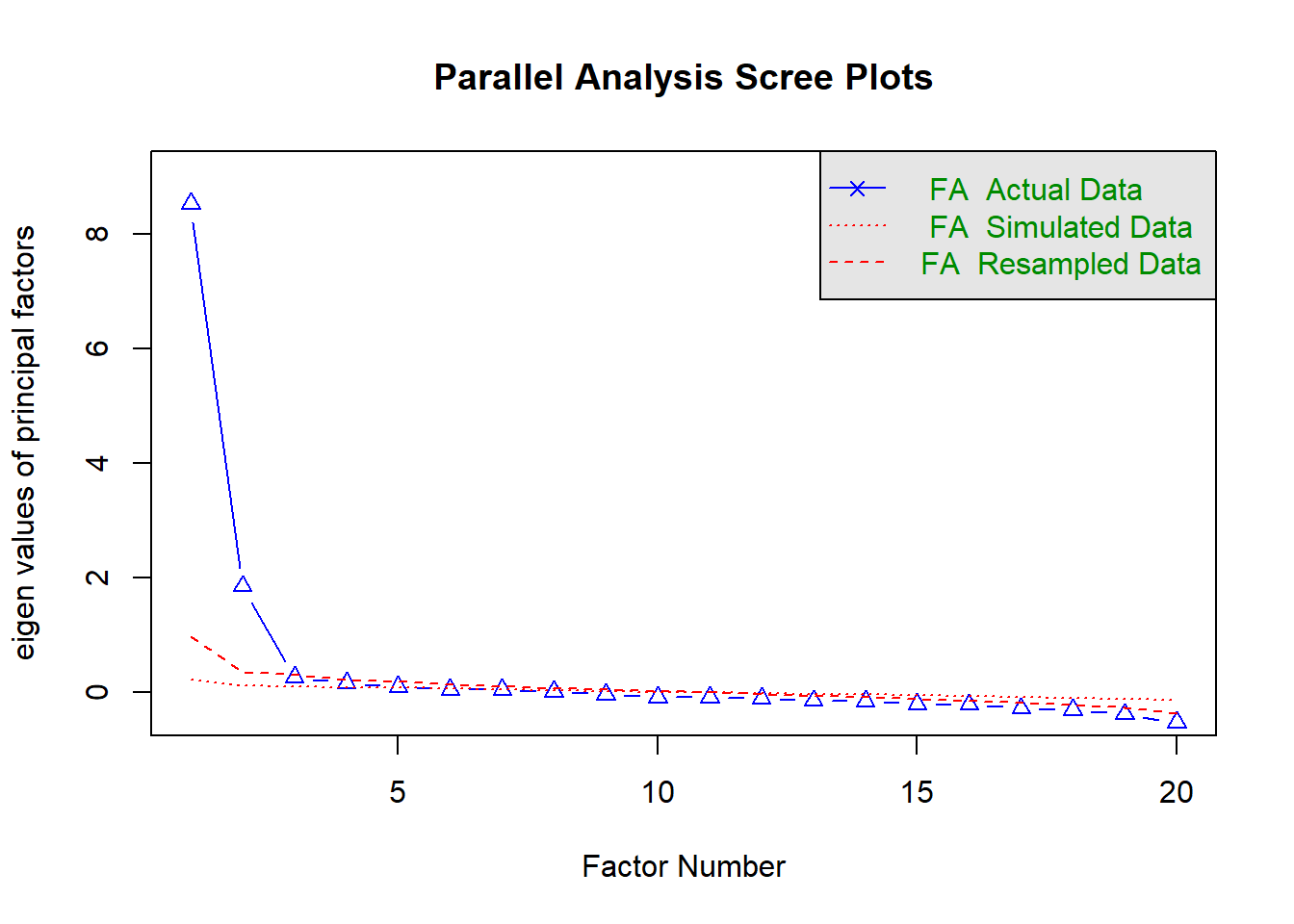
Parallel analysis suggests that the number of factors = 5 and the number of components = NA 4 Teoría Clásica de los Test: Ítems de selección de respuesta.
4.1 Análisis paso a paso de un test de selección de respuesta
En esta sección se presentará el análisis de un test de selección de respuesta paso a paso. El test que se utilizará será un subtest conformado por las primeras 20 preguntas del test de vocabulario de inglés.
Al igual que en todo test, el análisis de las propiedades de medición inicia estudiando la estructura de medición. En el caso del test de Vocabulario se tiene que el gráfico asociado al análisis paralelo sugiere cuatro factores, no obstante dos de ellos parecen irrelevantes.
Al examinar la varianza explicada por cada factor se observa que los factores 3 y 4 explican menors del 5% de la varianza de los ítems, por lo cual se va a trabajar únicamente con 2 factores.
WLS1 WLS2 WLS3 WLS4
SS loadings 6.0539242 4.5021013 0.89292358 0.35498570
Proportion Var 0.3026962 0.2251051 0.04464618 0.01774929Luego, se procede al análisis de las cargas factoriales. En el ejemplo de estudios la matriz de cargas factoriales indicó que el factor 1 tenía 12 ítems y el 2, 7 ítems. Además, se observó que el factor 2 es un factor de ítems fáciles. Por lo cual se consideró que el factor 1 representaba mejor el constructo de interés.
WLS1 WLS2
RC1 -0.10070398 1.000546253
RC2 0.51001481 0.195646346
RC3 0.17457682 0.699517332
RC4 0.58085197 -0.004133916
RC5 0.07562007 0.740607021
RC6 0.66120569 0.023649088
RC7 0.09050560 0.208472714
RC8 0.74159206 0.077027393
RC9 0.77825989 -0.008041313
RC10 -0.03544667 0.866424267
RC11 0.28521571 0.585483342
RC12 0.59210097 0.215669651
RC13 0.71093640 0.096653824
RC14 0.09832074 0.644362926
RC15 0.48034625 0.146579319
RC16 0.01396117 0.705435531
RC17 0.57566549 0.260413327
RC18 0.77104458 -0.099987404
RC19 0.83596254 -0.146970843
RC20 0.81100660 -0.029765238Luego se procede al análisis de las estadísticas de los ítems. En el ejemplo el alfa de Crobach fue de 0.84 y los estadísticos de los ítems presentaron valores apropiados, por lo cual todos pueden ser utilizados apra la estimación de las puntuaciones de los individuos.
[1] 0.8354046 item Dific Discrim Alfa red
1 P2 0.68 0.54 0.83
2 P4 0.21 0.47 0.83
3 P6 0.61 0.59 0.82
4 P8 0.55 0.69 0.81
5 P9 0.49 0.68 0.82
6 P12 0.70 0.61 0.82
7 P13 0.62 0.65 0.82
8 P15 0.61 0.52 0.83
9 P17 0.72 0.60 0.82
10 P18 0.24 0.56 0.83
11 P19 0.18 0.53 0.83
12 P20 0.50 0.69 0.81Note que las preguntas más difíciles son P4 y P19. La P4 tiene las opciones: finish embellish cap squeak talk, mientras que la P19 tiene las opciones: cistern crimp bastion leeway pleat.
Finalmente, se procede a estimar los intervalos de confianza de las personas evaluadas, por medio de la suma y resta de la constante \(Z_{1-\alpha/2}\sigma_{\varepsilon}\), con: \[\hat{\sigma}_\varepsilon=\hat{\sigma}_X\sqrt{1-\hat{\rho}_{XX'}}\]
En el caso del ejemplo, se obtuvo que \(\hat{\sigma}_X\) fue 3.32, por lo cual la constante para el IC95% sería \[1.96\cdot3.32\sqrt{1-.84}=2.60\]
4.2 Análisis de opciones
Observe esta pregunta del DIMA sobre fórmulas notables: ¿Cuál es el resultado de \((x^2+2y)^2\)? Las opciones de esta pregunta son
- $x^4-4x^2y+4y^2$
- $x^4+2y^2$
- $x^4+4x^2y+4y^2$
- $x^4+4y^2$
- No sé la respuesta opc Q1 Q5
1 1 3.7 2.7
2 2 34.0 4.0
3 3 8.1 83.2
4 4 41.5 9.9
5 5 12.8 0.2En el test de vocabulario de los archivos adjuntos se tiene que en la Pregunta P4 (finish embellish cap squeak talk, clave=1x1xx), se presentaron los siguientes porcentajes de selección de opciones, dentro de los dos quintiles de interés.
Q
Q1 Q5
11xxx 9.94 10.73
1x1xx 1.96 47.64
1xx1x 0.84 0.13
1xxx1 0.00 0.00
x11xx 0.98 2.30
x1x1x 3.22 0.38
x1xx1 1.68 4.47
xx11x 0.56 0.00
xx1x1 0.28 0.00
xxx11 18.07 27.08
xxxx1 4.62 0.13
xxxxx 57.84 7.15Note que una respuesta que llama mucho la atención es la combinación xxx11: squeak- talk .
4.3 Equiparación
Una situación que puede darse en la aplicación de exámenes es que se requieran aplicar distintas versiones de un examen. Esta situación puede llevar a que un grupo realice una versión más difícil que otro, lo cual lo podría poner en desventaja. Debido a esto se requiere utilizar un método de equiparación, es decir, un método que permita llevar las notas de un formulario a la escala del otro.
A continuación se presentarán dos métoso que permiten realizar equiparaciones. Estos métodos requieren el uso de dos conceptos:
- Grupos equivalentes: Grupos de población con caracteríticas similares en la habilidad evaludada. Se pueden obtener si se recurre al azar.
- Anclaje: Ítems que comparten las distintas versiones del test.
Para realizar una equiparación relativamente directa se requiere de grupos equivalentes e ítems de anclaje en las fórmulas.
En los ejemplos siguientes se utilizará como base el siguiente caso, basado en una división de la base de vocabulario. La base se dividió en tres fómulas de 12 preguntas con grupos reducidos de personas.
- Test 1: Personas 1 a la 1000. Anclaje XY= primeras 4 preguntas.
- Test 2: Personas 1001 a la 2000. Anclaje XY primeras 4 preguntas. Anclaje YZ= últimas 4 preguntas.
- Test 3: Personas 2001 a la 2739. Anclaje YZ=últimas 4 preguntas.
En las siguientes líneas se mostrará la equiparación del test 2 a la escala del test 1. Los promedios observados en los test 1 y 2 fueron:
[1] 6.084 5.230Mientras que los de sus anclajes fueron:
[1] 1.614 1.626Note que en los anclajes se obtuvieron notas similares, pero en las notas totales parece haber una ventaja a favor del grupo que tomó el test 1.
En función de lo anterior se buscará llevar las notas del test 2 a la escala del test 1.
4.3.1 Método de la transformación lineal
Suponga que se tienen unas notas \(X\) que se desean transformar a la escala de un conjuno de notas \(Y\). El valor nuevo de una nota \(x\) es el valor \(y\) que posea la misma punuación estandarizada que \(x\).
\[Y=\left(\frac{S_y}{S_x}\right)(X-\overline{X})+\overline{Y}\] En el ejemplo de trabajo, si se desea pasar la nota del test \(2\) a la escala del test \(1\), se tendría que el test 2 sería \(X\) y el test 1 sería \(Y\). Luego se aplicaa la fórmula indicada a la puntuación que se desea transformar. Si se desea tranformar el valor \(X=10\) y se sabe que \(\overline{X}=5.23\), \(S_X=3.28\),\(\overline{Y}=6.08\) y \(S_Y=3.29\), entonces \(Y\) sería:
3.29/3.28*(10-5.23)+6.08[1] 10.86454La equiparación de todas las notas observadas en el test 1, por medio del método de la transformación lineal, son las siguientes
Obs N TL N TL-A
1 0 0.8399703 0.8792804
2 1 1.8426528 1.8797571
3 2 2.8453354 2.8802338
4 3 3.8480179 3.8807105
5 4 4.8507005 4.8811872
6 5 5.8533830 5.8816639
7 6 6.8560656 6.8821406
8 7 7.8587481 7.8826172
9 8 8.8614307 8.8830939
10 9 9.8641132 9.8835706
11 10 10.8667958 10.8840473
12 11 11.8694783 11.8845240
13 12 12.8721608 12.8850007Note que la variación debida al banco constante es baja, esto se debe a que los grupos son equivalentes. Ahora bien, al grupo que le tocó el test más difícil, si se le ajustaron las notas.
4.3.2 Método equipercentil
En este método el valor nuevo de una nota \(x\) es el valor \(y\) que posea el mismo percentil que \(x\). En el ejemplo de trabajo, si se quiere transformar la nota \(x=10\) del test 2 a la escala del test 1 se haría lo siguiente
#Cálculo de la frecuencia relativa acumulada de la nota estudiada
#Esto es, inverso del percentil
p<- length(T2[T2<=10]) / (length(T2) + 1)
#Cálculo del valor del percentil en la escala de interés
quantile(T1,p) 92.70729%
11 Las notas con la trasnformación equipercentil son las siguientes:
Obs N Equip N Equip-A
1 0 0.3235294 0.3159393
2 1 1.6493506 1.6536676
3 2 2.8446602 2.8734528
4 3 3.8944444 3.9564449
5 4 5.0872093 5.1786749
6 5 6.1179245 6.2006792
7 6 7.0270270 7.1306954
8 7 8.1179775 8.1652147
9 8 9.1052632 9.1120933
10 9 9.8913043 9.8850263
11 10 10.5468750 10.5394161
12 11 11.2734375 11.2748455
13 12 12.0972222 12.1016975En rojo están las notas de la equiparación por la transformación lineal y en azul, las notas de la equiparación por el método equipercentil.
4.3.3 Grupos No Equivalentes
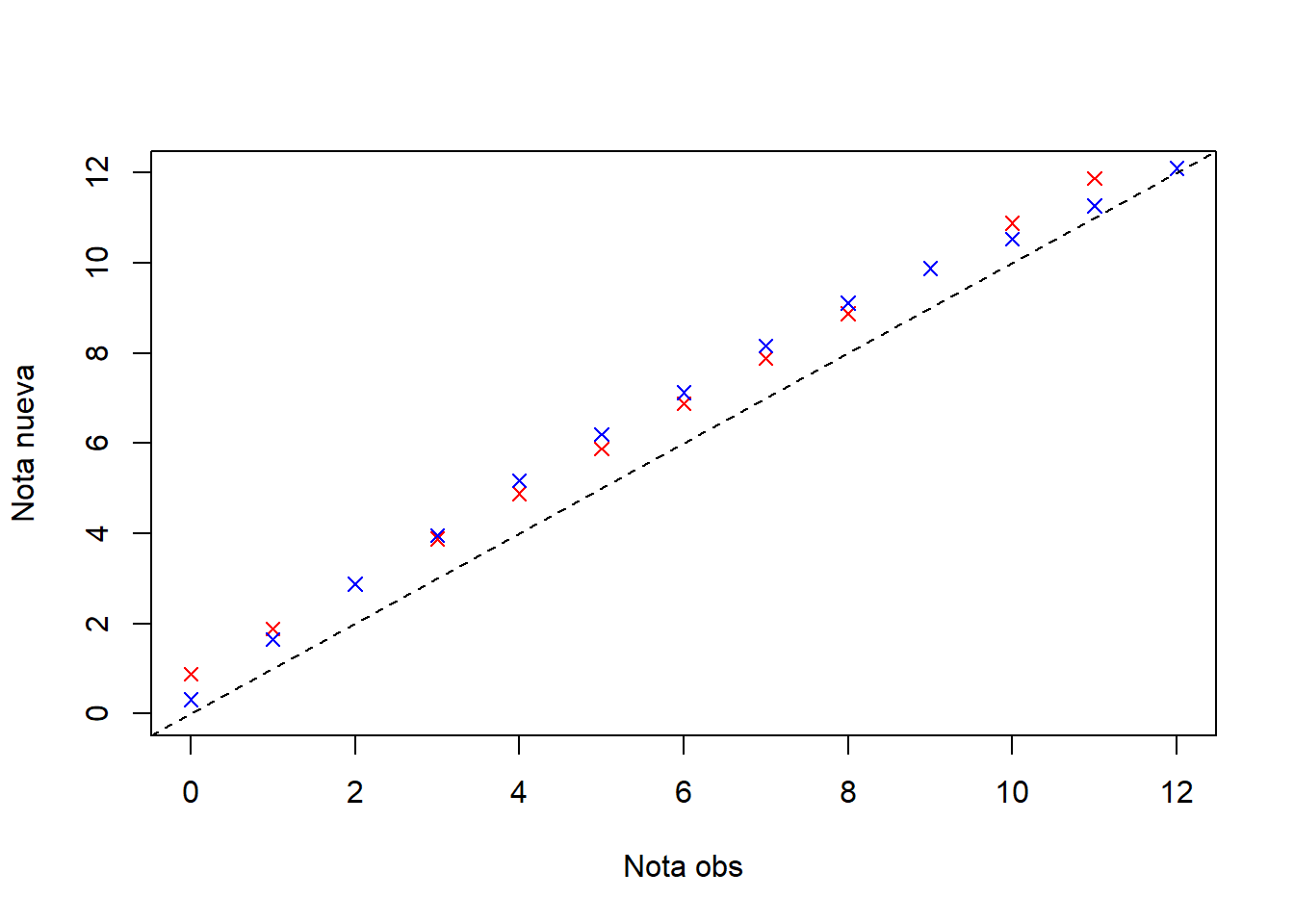
En el caso de grupos no equivalentes, el anclaje se vuelve mucho más relevante, debido a que las puntuaciones totales tienen distrubuciones distintas a la de la población. Por ejemplo, los percentiles en un grupo de habilidad baja podrían estar sobreestimados, mientras que en un grupo de habilidad alta podrían estar subestimados.
Ejemplo: Considere la división en la que el test 1 se aplicó a las 1000 personas preeestablecidas en la que el inglés no es la lengua materna, contra un grupo de 1000 personas con lengua materna inglés, a los cuales se les aplicó el test 2.
Si se equiparan las notas del grupo del test 1 a la escala del test 2, podría darse una sobreestimación de las notas, debido a que el segundo grupo tiene una distribución concentrada en notas altas debido a su alta habilidad. Nótese que sus promedios son distintos, pero no debido a la dificultad de la fórmula, sino a sus habilidades:
[1] 6.084 8.351En estos casos, el uso de un anclaje se vuelve relevante, lo cual se ve en las diferencias entre las puntuaciones otorgadas por los métodos sin y con anclajes.
Obs N Equip N Equip-A N Equip N Equip-A 2
1 0 1.233333 -0.36821705 2.893667 -0.7581164
2 1 2.908163 -0.01152638 3.790665 0.2390364
3 2 4.390244 0.68436461 4.687662 1.2361893
4 3 5.940789 2.19320317 5.584660 2.2333422
5 4 7.183544 3.01432755 6.481657 3.2304951
6 5 8.111650 3.80258803 7.378655 4.2276479
7 6 8.951613 4.98252010 8.275652 5.2248008
8 7 9.653846 5.96694111 9.172650 6.2219537
9 8 10.223776 6.90204845 10.069647 7.2191065
10 9 10.832278 8.05273172 10.966645 8.2162594
11 10 11.424051 9.30371017 11.863642 9.2134123
12 11 11.992537 10.68039319 12.760640 10.2105651
13 12 12.365672 11.91137012 13.657637 11.2077180En rojo están las notas de la equiparación por la transformación lineal y en azul, las notas de la equiparación por el método equipercentil. Note que las notas del grupo de no hablantes nativos del inglés más bien son más bajas que las iniciales, esto se debe a que el test 1 era más fácil que el 2.
4.4 Código R de análisis de opciones
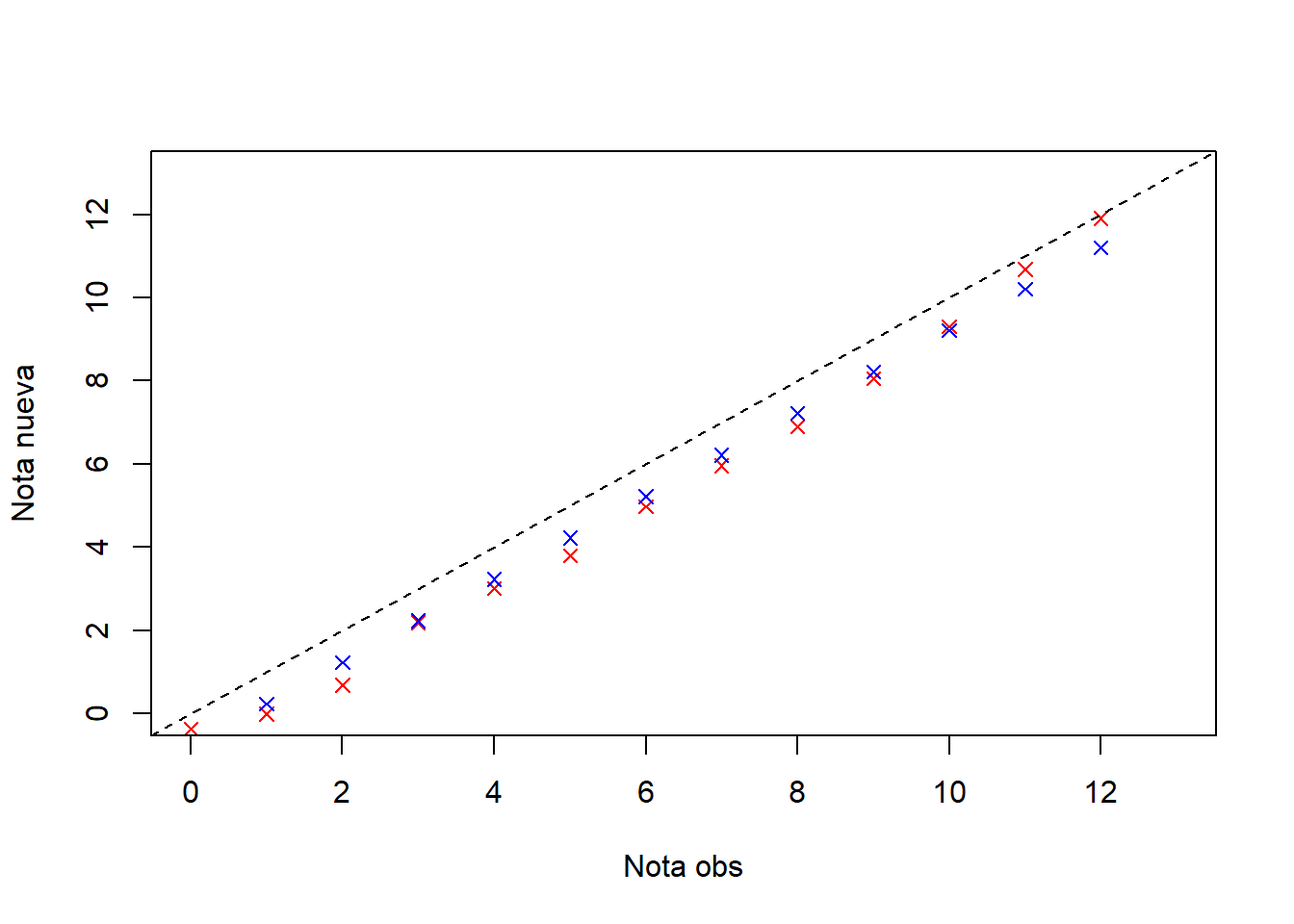
Cargar la base de trabajo
BASE<-read.csv("Vocab.csv")Definir dos bases: una con el conjunto de ítems calficados (ITEMS) y otro con los ítems con sus claves originales (ITEMSr)
ITEMS<-BASE[,c(2, 4, 6, 8, 9, 12, 13, 15, 17:20)+80]
ITEMSr<-BASE[,c(2, 4, 6, 8, 9, 12, 13, 15, 17:20)]Calcular la nota del test y una tabla con la distribución de las notas de las personas de los quintiles 1 y 5, según respuesta seleccionada.
Nota<- rowSums(ITEMS)
## Indicar el quintil de las personas
q1<-quantile(Nota,.20)
q4<-quantile(Nota,.80)
NotaG<-Nota
NotaG<-NA
NotaG[Nota<=q1]<-"Q1"
NotaG[Nota>=q4]<-"Q5"
#Distibución de los quintiles según opción
item<-ITEMSr[,4] ## DEFINIR ÍTEM
round(prop.table( table(item,NotaG), margin=2),3)*1004.5 Código R de equiparación
Conformación de las bases de trabajo. En este caso vamos a descomponer una base existente para simulara bases de 3 fórmulas, pero lo normal es tener una base para cada fórmula.
BASE<-read.csv("Vocab.csv")
## Delimitación a personas hablantes no nativas del inglés
BASE<-subset(BASE,engnat==2)
## Cada base posee 24 columnas, 1:12 las respuestas seleccionadas y 13:24 la codificación correcta/incorrecta
BASE1<-BASE[1:1000 ,c(17:20,2, 4, 6, 8, 9, 12, 13, 15 ,c(17:20,2, 4, 6, 8, 9, 12, 13, 15 )+80 )]
BASE2<-BASE[1001:2000 ,c(17:21,24,25,29, 27:28, 33:34,c(17:21,24,25,29, 27:28, 33:34 )+80 )]
BASE3<-BASE[2001:2739 ,c(36:43,27:28,33:34,c(36:43,27:28,33:34 )+80)]Crear bases con los ítems calificados con ceros y unos.
Test1<-BASE1[,13:24]
Test2<-BASE2[,13:24]Cálulo de las notas totales (T1 y T2) y cálculo de las notas del anclaje (A1 y A2)
T1<-rowSums(Test1)
T2<-rowSums(Test2)
A1<-rowSums(Test1[,1:4]) # UBICACIÓN DE LOS ÍTEMS ANCLA
A2<-rowSums(Test2[,1:4]) # UBICACIÓN DE LOS ÍTEMS ANCLALibrería y preparación de los datos para realizar equiparación
library(equate)
n1 <- freqtab(data.frame(T1,A1)) #total, anchor
n2 <- freqtab(data.frame(T2,A2))
#Si no hay anclaje solamente no se reporta:
#n1 <- freqtab(T1) #total, anchor
#n2 <- freqtab(T2)Equiparación del test 1 a la escala de del test 2, por el método Lineal y usando anclaje.
## El primer test es el que se va a equiparar
## El segundo test es la escala que se va a usar
ResLin<-equate(n2, n1, type = "linear", method = "tuck")
ResLin$concordance[,1:2]Equiparación del test 1 a la escala de del test 2, por el método Equipercentil y usando anclaje.
ResEq<-equate(n2, n1, type = "equip", method = "freq")
ResEq$concordance[,1:2]Gráfico
plot(ResEq$concordance[,1],ResEq$concordance[,3],xlab="Nota obs", ylab="Nota nueva", col="red")
abline(0,1)4.5.1 Guía de trabajo 3
- Realice un análisis psicométrico de los ítems, con la TCT, de los ítems de la BASE03 [6 puntos].
- Justifique por qué se puede concluir que la base presenta una estructura unidimensional.
- Identifique los ítems que cargan en el factor 1.
- Calcule la dificultad y discriminación de los ítems que evalúan el constructo pretendido.
- Estime el alfa de Cronbach con los ítems con propiedades psicométricas apropiadas.
- Estime el IC95% de una persona con una nota de 10 unidades [2 puntos].
Presente la frecuencia de selección de opciones del ítem más difícil de la base [1 punto].
Comente cómo fue el comportamiento de la clave del ítem de la pregunta seleccionada. Indique cuál es el distractor más atractivo para la población de baja habilidad (sin considerar el no respondo o el error de marcación) y trate de brindar una explicación con base en el análisis de las respuestas reales. Mencione si hay un distractor llamativo para las personas de alta habilidad [3 puntos].
Calcule la nota total y la de anclaje de los sujetos del test 2 y el test 3. Presente los promedios y desviaciones estándar de las cuatro variables [2 puntos].
Realice la equiparación lineal de las notas con el promedio más bajo a la escala del folleto con el promedio más alto. Presente un gráfico de las notas nuevas contra las originales [4 puntos].
Realice la equiparación equipercentil de las notas con el promedio más bajo a la escala del folleto con el promedio más alto. Presente un gráfico de las notas nuevas contra las originales [4 puntos].
Analice la magnitud de los cambios de las notas con las equiparaciones realizadas [2 puntos].